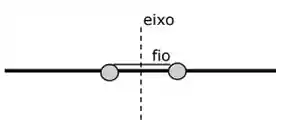
O experimento da figura consiste de uma haste horizontal delgada de comprimento 0,60 m que pode girar livremente em torno do eixo vertical que passa pelo seu C.M. O momento de inércia da haste em relação ao eixo é de 0,0060 kg.m2. Duas pequenas esferas (partículas) cada uma de massa 0,10 kg podem deslizar pela haste através de um furo existente em cada uma. Inicialmente, as esferas estão a uma distância 0,20 m e simetricamente colocadas em relação ao eixo de rotação e mantidas nestas posições mediante um fio que as une. Este sistema gira em torno do eixo com velocidade angular 12 rpm quando o fio é queimado por uma chama, as esferas deslizam até as extremidades da haste. Qual é a velocidade angular final do sistema?

a) 1,2 rpm

b) 1,3 rpm

c) 2,2 rpm

d) 4,0 rpm

e) 5,6 rpm

Essa questão é a cara de conservaçõ de momento angular, né? A gente tem o momento inicial, podemos calcular o momento de inércia final e assim calcularmos a velocidade angular final do sistema, sacou? Então:

Agora vamo calcular o momento de inércia depois (que vai ser a soma do momento de inércia das duas partículas). Como as partículas tem mesma massa e mesma distância ao eixo de rotação (simétricos), temos:

Então aplicando na fórmula da conservação de momento, temos:

Show de bolaaaa!