Em uma vareta rígida de comprimento e massa desprezível estão presas três bolinhas idênticas de massas iguais . Duas delas encontram-se unidas no centro da vareta enquanto a outra está fixa na sua extremidade. Considere que o raio das bolinhas é muito pequeno comparado com a distância . O sistema de varetas-bolinha gira com velocidade angular constante, em um plano horizontal sem atrito, em torno de um eixo que passa pelo ponto . A figura mostra o sistema visto de cima no instante . Em um certo instante de tempo posterior, uma das bolinhas do centro se solta e escorrega pela vareta pela vareta até se prender à bolinha da extremidade.

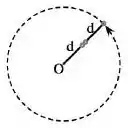
O sistema permanece girando mas passa a se mover com velocidade constante em módulo dada por:

a)

b)

c)

d)

e)

Passo 1

Passo 2

Resposta