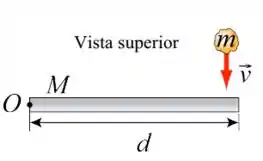
Uma haste fina de massa e comprimento , inicialmente em repouso, pode girar horizontalmente sobre uma mesa, sem atrito, em torno do ponto O, como mostra a figura. Um pedaço de massa de vidraceiro de massa , com velocidade , colide com a haste em uma das extremidades, permanecendo grudado nela.
- Qual é o momento angular do sistema haste+massa imediatamente antes da colisão?
- Qual é a velocidade angular do sistema imediatamente após a colisão?
- Qual é a razão entre a energia cinética do sistema haste+massa depois e antes da colisão?
Dado: O momento de inércia de uma haste de massa M e comprimento d em relação a um eixo que passa pelo seu centro de massa é
Passo 1
a):
O momento angular será o momento angular que a partícula que tava caindo tinha. Isso é:
Ou:
Como:
Então:
Passo 2
b):
Pra achar isso vamos usar a conservação de momento angular, isso é:
Bom:
O momento de inercia final vai ser a soma do momento de inercia da barra em relação ao pino e o momento de inércia da partícula.
Como a barra não está girando ao redor do centro de massa, vamos usar o teorema dos eixos paralelos:
Então:
Então:
Assim:
Passo 3
c):
A energia cinética antes é dada por:
E:
E:
Então:
E a energia cinética final é:
Com:
E como:
Então:
Então:
Resposta
a):
b):
c):