Considere as seguintes afirmações:
(I) A aceleração do centro de massa de um corpo rígido é igual ao quociente da força externa resultante pela sua massa total, desde que o corpo não tenha movimento de rotação.
(II) Um disco de raio gira em torno de seu eixo com uma aceleração angular . O módulo da aceleração de um ponto sobre as suas bordas vale .
(III) A energia cinética de um corpo rígido que apenas gira em torno de um eixo fixo depende somente da massa total e da velocidade angular do corpo.
(IV) Quando a força resultante sobre um corpo rígido é nula, não pode haver torque em relação ao seu centro de massa.
(V) A força resultante sobre um corpo rígido em rotação pura em torno de um eixo fixo no espaço e que passa pelo seu centro de massa é sempre nula.
(VI) Quando a velocidade do centro de massa de um sistema de partículas é nula, o seu momento angular é independente do ponto do espaço escolhido como referência.
(VII) Um corpo pode girar sem estar sujeito à ação de um torque.
Passo 1
POW! Nesse exercício, que tal analisarmos item a item e verificar qual que é verdadeiro ou qual que é falso?
Pelo visto, o assunto é rotação dos corpos rígidos. Então, com o papel e caneta na mão... Partiu!
Passo 2
ITEM (I)
Cara, imagina um corpo rígido qualquer de massa e com várias forças externas...
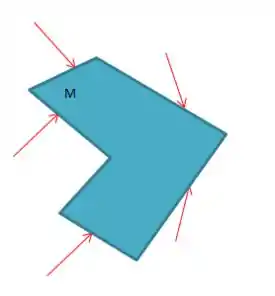
Somando todas essas forças vetorialmente falando, vamos ter uma resultante sendo aplicada no centro de massa desse corpo...
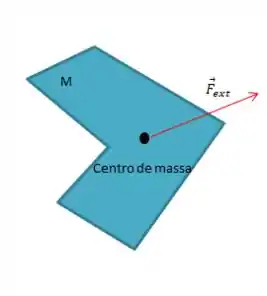
Se esse corpo estiver livre para girar e também para se transladar (andar de um lado para o outro). Cara, de acordo com Newton, vai surgir aí querendo ou não uma aceleração do centro de massa resultante...
Que independe se o corpo está girando ou não!
Então, esse item está ERRADO, por ele impor “desde que o corpo não tenha movimento de rotação” o que não é verdade.
Passo 3
ITEM (II)
Cara, quando um disco está girando com velocidade tangencial ...
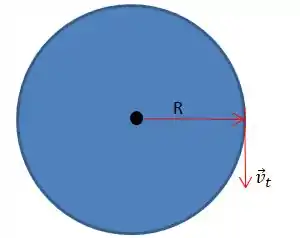
E só pelo fato de ter rotação vai existir força centrípeta...
Se a velocidade tangencial estiver aumentando ou diminuindo (em módulo) vai existir aceleração tangencial cujo módulo vai ser...
Então veja que falar que a aceleração em um ponto da borda é não é bem verdade, pois quando falamos de aceleração e não especificamos se é tangencial ou centrípeta, é porque estamos nos referindo à aceleração total .
Então esse item também é FALSO.
Passo 4
ITEM (III)
ORA! Falso, neh? Afinal de contas a energia cinética de um corpo rígido que apenas gira em torno de um eixo fixo, depende do momento de inércia e não da massa:
Onde é a velocidade angular.
Passo 5
ITEM (IV)
POW! Falso, neh? Pensa no seguinte corpo rígido e as seguintes forças...
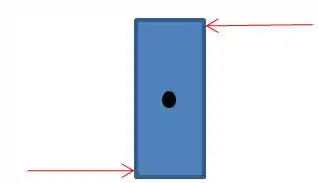
Repare que a força resultante nele é nula, mas o torque não afinal o corpo vai tender a girar .
Passo 6
ITEM (V)
CERTÍSSIMO! Kkkk
O centro de massa vai estar acelerado se a existir força externa, como vimos no passo 1. E se a força externa total se anular, então o centro de massa não vai estar acelerado. Mas o corpo ainda pode girar, como no passo anterior.
Passo 7
ITEM (VI)
CERTÍSSIMO também!
O momento angular é dado por...
Onde é a velocidade do centro de massa. Se ela é nula, então o momento de inércia que é independente do ponto escolhido.
Passo 8
ITEM (VII)
Ora! Assim como uma partícula pode se mover sem ter força (basta mover com velocidade constante), então um corpo também pode girar sem ter torque resultante. Basta girar com velocidade angular constante .
CORRETO
Resposta
Quantidade de itens corretos: 3