Corpos Rígidos, Rotação, Dinâmica de Rotação, Momento Angular
Um carrossel em forma de disco sólido homogêneo, com massa e raio , está fixo em seu centro de massa por um eixo vertical e pode girar sem atrito no plano horizontal. Partindo do repouso, o carrossel é submetido a uma aceleração angular constante de no sentido anti-horário, até atingir uma velocidade angular .
Determine o deslocamento angular realizado pelo carrossel durante seu processo de aceleração e o tempo necessário até atingir sua velocidade angular final.
Cessada a aceleração, o carrossel se mantém com velocidade angular de . Um menino de massa , correndo com uma velocidade na direção mostrada na figura, tal que , salta sobre a borda do carrossel e se agarra a ele. Modele o menino como uma partícula.
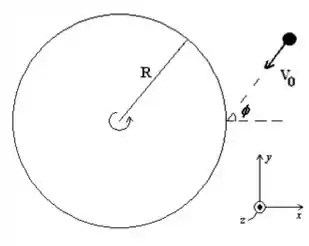
Determine os vetores angular do menino e do carrossel, respectivamente e , imediatamente antes do salto do menino sobre o carrossel(use o sistema de coordenada mostrado na figira).
Determine a velocidade angular final do conjunto carrossel menino e o sentido da rotação (horário ou anti-horário) após o menino saltar no carrossel.
Passo 1
Para o item , precisamos lembrar das equações de movimento para movimento circular!
Vamos primeiro descobrir quanto tempo o carrossel demorou até atingir uma velocidade de , para isso vamos usar:
Passo 2
Agora que temos o tempo podemos descobrir o deslocamento:
Passo 3
Para determinar os momentos angulares, vamos relembrar sua definição, . Para o menino, teremos:
Pois, é a distância que o menino estará do eixo no momento da colisão. A direção e o sentido do vetor é dado pela regra da mão direita! Substituindo, temos:
Passo 4
Para o carrossel, devemos lembrar da seguinte definição, , agora sim podemos achar o momento angular do carrossel!
Substituindo, temos:
A direção e o sentido do vetor é dado pela regra da mão direita!
Passo 5
Para achar a velocidade angular do conjunto carrossel menino, iremos recorrer à conservação do momento angular! Mas lembre-se que o momento angular só se conserva quando não existem torques externos! Ah...beleza! Então a gente pode sim usar a conservação para resolver esse item! Então vamos lá!
Como a gente já calculou os momentos angulares antes de o menino saltar, fica bem mais fácil!
Isolando a velocidade angular final, temos:
Resposta