Considere um disco de massa e raio girando com velocidade tangencial em torno de um eixo horizontal que passa pelo seu centro. Forneça os itens abaixo em termos de , ou .
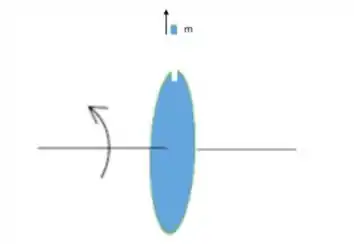
a) Calcule a energia cinética e o módulo do momento angular do disco. Mostre explicitamente o cálculo de todas as quantidades necessárias para obter estas grandezas.
b) Suponha que um pedaço do disco de massa quebra e sobe verticalmente acima do ponto do qual se desprendeu. Calcule a altura que ele sobe antes de começar a cair.
c) Qual a velocidade angular final do disco quebrado?
d) Considere o disco intacto girando em torno de um eixo paralelo ao anterior a uma distância . Calcule a razão da inércia rotacional anterior em relação a esta nova.
Passo 1
Fala galerinha, beleza? Partiu resolver esse problema sobre rotações!
O item (a) é bem simples: basta calcular a energia cinética e o momento angular. A energia cinética de um corpo em rotação é
O momento de inércia do disco é
Já a velocidade angular se relaciona com a velocidade tangencial por
Assim,
Portanto,
Já para o momento angular, temos
Assim,
Passo 2
Agora vamos para o item (b)! A velocidade do pedacinho de massa no momento que “foge” do disco é . Com isso, é só usar um pouquinho de cinemática para achar a altura máxima atingida:
No ponto de altura máxima temos , de modo que
Passo 3
Para achar a velocidade angular do disco após a saída do pedacinho de massa , vamos usar a conservação do momento angular:
Antes, o momento angular era
Após a desprendimento, temos
Logo,
O momento de inércia é o momento de inércia menos o momento de inércia de uma partícula pontual de massa a uma distância do eixo de rotação (corresponde ao pedacinho de massa ):
Com isso, podemos escrever
Isolando :
Passo 4
Para o item (d), voltamos a situação do disco inteiro, sem o pedacinho solto. Ele pede a razão dos momentos de inércia entre a situação que o eixo de rotação está no centro de massa do disco e da situação em que esse eixo está a uma distância do centro de massa:
Sabemos que
Usando o teorema dos eixos paralelos, temos que
Com isso,
Portanto,
Ufa, deu um trabalhinho mas chegamos ao fim 😊!