Corpos Rígidos, Dinâmica de Rotação, Momento Angular ,Trabalho e Energia Cinética
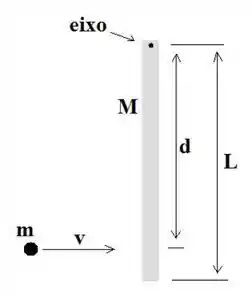
A figura mostra uma barra homogênea pendurada, de comprimento e massa , que gira em torno de um eixo numa de suas pontas. A barra, inicialmente em repouso, é atingida por uma partícula de massa num ponto abaixo do eixo. Admita que a colisão é perfeitamente inelástica. Qual deve ser a velocidade da partícula para que, após a colisão, o ângulo máximo entre a barra e a vertical seja de ?
Utilize .
Passo 1
Para determinar a velocidade da partícula para que a barra gire , iremos utilizar a Lei da Conservação do Momento Angular. Podemos utilizála pois não há torques externos ao sistema (partícula barra).
Lembrando que antes da colisão a barra está parada e que após a colisão, que é completamente inelástica, a partícula gruda na barra, temos:
em módulo, temos:
Passo 2
Para o sistema, temos o seguinte momento de inércia, sabendo que a colisão é perfeitamente inelástica, ou seja os corpos saem juntos! Utilizando o teorema dos eixos paralelos, temos:
Para o sistema, temos:
Passo 3
Substituindo na fórmula da conservação:
Isolando a velocidade angular, e substituindo os valores, temos:
Bom achamos a velocidade logo após a colisão! Legal...mas para que eu quero isso?!
Passo 4
Bom, agora que temos a velocidade logo após a colisão, podemos usar o Teorema do Trabalho e Energia Cinética!
Como queremos que a barra chegue a , sua velocidade angular final será zero! Se liga!
Achamos mais uma incógnita, mas ainda não é a resposta final! Mas continua ligado!
Passo 5
Agora temos o trabalho realizado, como sabemos que a única força que realizou trabalho foi a força peso da partícula e da barra, temos:
Ta ligado que a altura é quanto o centro de massa de cada componente deve subir para que a barra fique a da vertical!
Igualando as duas expressões para o trabalho, temos:
Agora é só substituir os valores:
Uffaaa....essa foi longa!
Resposta