Um disco de raio R = 2,0 m gira sem atrito no plano horizontal, ao redor de um eixo perpendicular à sua superfície e passando no seu centro. Seu momento de inércia em relação a esse eixo vale . Uma partícula de massa m = 1,0 kg, a uma distâancia R/2 do centro do disco, gira junto com este com velocidade angular = 3,0 rad/s.

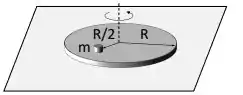
Num certo instante, a partícula escorrega e para novamente na borda do disco, a uma distância R do centro. Qual é a nova velocidade angular (em rad/s) do sistema disco + partícula?

a) 1,0

b) 1,5

c) 2,1

d) 2,2

e) 3,0

f) 3,5

g) 4,0

h) 4,4

Pela conservação de momento angular, temos:

Agora vamos calcular os momentos de inércia inicial e final. No começo temos:

E no final, ficamos com:

foi dado na questão, e vale 3rad/s, então é só jogarmos tudo na formulinha da conservação de momento!