Durante uma competição de bilhar, Efren Manalang Reyes, um dos melhores jogadores de todos os tempos, atinge a bola com o seu taco como indicado na figura . O taco exerce uma força constante (alinhada com o taco como mostra a figura A) durante um intervelo de tempo , produzindo na bola um impulso linear de módulo J. A bola (massa e raio ao ser atingida pelo taco não rococheteia e move-se em linha reta para a
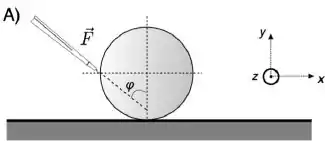
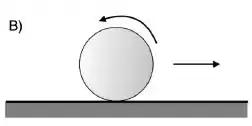
Direita, girando como indicado na figura B até um instante medido a partir do início do movimento. A partir desse instante de tempo, a bola começa a deslizar, sem girar, sobre a mesa até o instante a partir do qual começar a rolar sem deslizar. O coeficiente de atrito entre a bola e a mesa é .

Passo 1
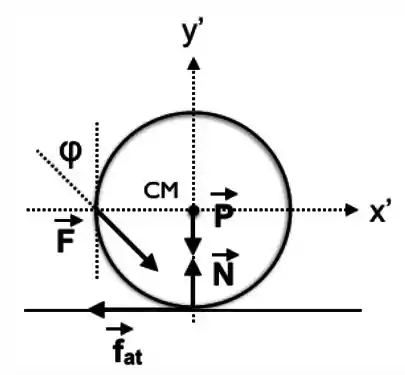
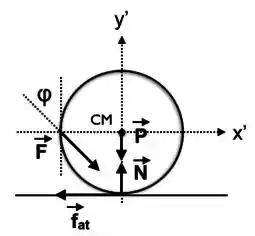
Forças no sistema de coordenadas
Torques:
Como as forças e tem o raio de ação em cima do centro de massa da roda elas não vao exercer torque.
Passo 2
Bom, vamos calcular a variação de momento linear através da força externa que age na bola, ok ?
Assim como a taxa de variação no tempo do momento angular vai ser igual ao torque nesse ponto
Assim, juntandos as forcas que temos ficamos com:
Trabalhando com a equacao do momento linear primeiro, ok
Como não há variação de velocidade no eixo x, temos que as forcas no eixo x vao se anular, ficando so as do eixo y
A velocidade inicial fica então
Agora voltando para a equação do momento angular, temos
Assim, isolando a velocidade angular a gente fica com
Passo 3
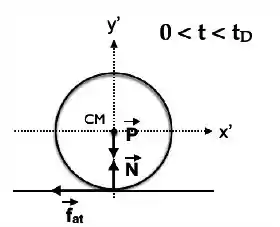
Vamos dividir a velocidade do centro de massa em translação e rotação
Rotação
Translação
Como a Normal e a força peso se anulam, vamos ter que a aceleração só vai existir no eixo, que vai ser feita pela força de atrito.
Da rotacao temos
Assim temos as equacoes de movimento
O instante que ela ta pedindo na questão e quando a roda para de girar
Passo 4
Letra d)
Calma que já ta acabando, ultima letra

Resposta
Letra a)
Letra b)
Letra c)
Letra d)