Um disco de massa e raio está apoiado sobre uma superfície plana. Um fio inextensível, de massa desprezível, encontra-se enrolado ao redor do disco, preso a um eixo vertical. Um corpo de massa é preso a uma das extremidades do fio, que passa por uma pequena polia de massa desprezível.
Supondo que o sistema é solto a partir do repouso, e que o disco gira sem atrito, determine:
(a) A magnitude da força de tração
(b) A magnitude, direção e sentido do momento angular do disco em relação ao seu centro em um instante de tempo .
(c) Imagine agora que passado um intervalo de tempo o fio perde contato com o disco. Após o fio perder contato, um weta (o maior inseto do mundo), com massa , pousa exatamente no centro do disco. Se o inseto passa a se deslocar ao longo do raio do disco com velocidade constante , qual é o módulo da velocidade angular do disco quando o inseto se encontra a uma distância r em relação ao centro do disco?
Passo 1
Parte da dificuldade é entender o que está acontecendo...
Temos um disco de massa sobre uma mesa. Esse disco tem um fio enrolado sobre ele e esse fio está sendo puxado por um corpo de massa .
Resumindo a situação, o que acontece é isso aqui:
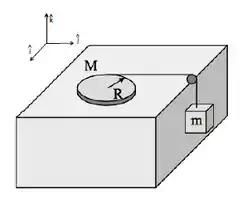
Passo 2
Na letra (a), queremos a tração no fio.
Se não tivesse nenhuma resistênica, o bloquinho desceria com a aceleração da gravidade.
Porém, como o movimento do bloquinho faz o disco entrar em rotação, quanto mais “difícil de entrar em rotação” esse disco for, mais tensionado esse cabo vai estar.
Essa dificuldade de entrar em rotação é o momento de inércia do disco , quanto maior esse , maior a força de tração.
Para achar essa força de tração, devemos analisar as forças tanto sobre o disco quanto sobre o bloquinho.
Passo 3
Começaremos com o bloquinho, que é mais simples:
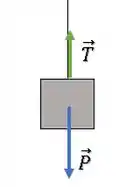
Como o bloquinho está descendo, a força resultante é na direção da força peso:
Agora, vamos ao disco. Ele também terá uma força peso e uma normal na vertical, elas estão aplicadas no centro de massa do disco e vão se cancelar.
Porém, estamos mais interessados nas forças horizontais do disco (olhando de cima):
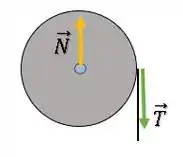
Como o centro de massa do disco se mantém em repouso, as forças ainda se cancelam:
Entretanto, a força vai gerar um torque no disco, e fazê-lo entrar em rotação, enquanto a força não gera torque pois está no centro de massa do disco. Por isso, vamos escrever a segunda lei de Newton para rotação:
Pelo formulário, sabemos que o momento de inércia de um disco em relação ao seu centro de massa é:
Passo 4
Agora, vamos juntar essas duas equações para achar a força de tração :
A única relação entre os dois é o próprio que queremos achar...
Então, vamos tirar outra relação da cartola.
Como o fio não desliza com o disco, podemos relacionar as acelerações linear do bloco e angular do disco assim:
Substituindo isso na segunda equação, temos:
Substituindo na primeira:
Passo 5
Na letra (b), queremos o vetor momento angular .
Momento angular pode ser calculado por:
Mas quem é a velocidade angular ?
Passo 6
Lembra que quando a força é constante cte em um objeto, podemos calcular sua velocidade com:
Para rotações, fazemos parecido. Como o torque é constante cte, podemos achar a velocidade angular do disco com:
O disco parte do repouso, então :
Além disso, temos que:
Então:
Passo 7
Substituindo novamente na expressão do momento angular, temos:
Agora, podemos susbtituir o valor de que achamos no item (a):
Achamos o módulo de , mas precisamos da direção e sentido também.
O vetor momento angular tem o mesmo sentido do vetor velocidade angular :
Agora, vamos olhar novamente para o disco:
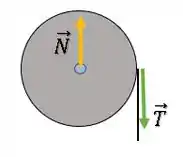
O disco gira no sentido horário.
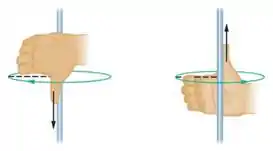
Pela regra da mão direita, o vetor estará na direção vertical para baixo, assim como o vetor .
Você pode explicar com palavras como está nessa frase acima, ou então, definir um sistema de eixos no desenho, como foi feito na letra (a) e escrever o vetor:
Passo 8
Na letra (c), temos que o fio já se desenrolou todo, então não há mais um torque sendo aplicado no disco e ele passa a girar com velocidade constante.
Como não há mais nenhum torque externo no disco, inclusive quando o inseto pousa, pois isso ocorre no centro do disco, o momento angular do disco vai se conservar:
Já calculamos o momento angular do sistema após um período de tempo:
Já no instante final, o momento angular será:
é o novo momento de inércia do conjunto disco mais inseto:
Então:
Passo 9
Igualando os dois momentos angulares, temos:
Assim, conseguimos a velocidade angular :
Resposta
(a)
(b)
(c)