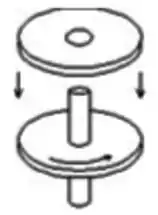
Uma roda, com momento de inércia , montada em um eixo com momento de inércia desprezível, está girando com velocidade angular . Uma roda não giratória, com momento de inércia , é subitamente encaixada no mesmo eixo, como mostrado. A combinação resultante das duas rodas e do eixo girará com velocidade angular:
a)
b)
c)
d)
e)
Passo 1
Tá sentindo o cheiro ?? Eu tô, e é cheiro de questão de conservação do momento angular.
Olha pra questão, e repara que você tem um corpo rotacionando, esse corpo vai sofrer uma alteração no seu momento de inércia e então ela pergunta a nova velocidade de rotação. Isso é a receita de bolo pra questão de conservação de momento angular. Então se viu uma questão assim, já começa a suspeitar.
Conservando o momento angular, temos:
Resposta
Letra e)