Um haltere é formado por duas partículas de massa (1 e 2) ligadas por uma haste rígida, de massa desprezível e comprimento . O haltere pode deslizar sem atrito sobre uma mesa. Uma partícula 3 de massa , com velocidade inicial (perpendicular à haste do haltere) colide com uma das partículas, como mostrado na figura.Sendo a colisão perfeitamente elástica, determine

a) Imediatamente após a colisão, a velocidade linear das partículas 2 e 3 (indicando a direção e sentido).
b) O impulso sofrido pela partícula 2.
c) Após a colisão, qual a velocidade linear do centro de massa do haltere?
Passo 1
a)
Quando nessa a vamos só considerar as massas de como uma colisão elástica normal, como aquelas que a gente ta cansado de fazer. Saca só!
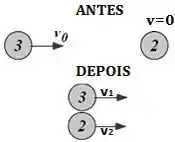
Pela conservação do momento linear, teremos:
Passo 2
Como a colisão é elástica, podemos usar a conservação da energia cinética. Na forma...
Dividindo essa equação pela equação que achamos no Passo 1, teremos:
Ah! Só pra lembrar. . Assim...
Passo 3
Agora é só fazer o sistema linear com as equações lineares das velocidades que achamos. São elas:
Somando as equações, teremos:
:D
Passo 4
b)
Pelo Teorema do Impulso-Variação do Momento Linear, teremos:
Como , teremos:
Passo 5
c)
Agora é só fazer a mesma coisa da “a” só com com o “sistema haltere”, que pesa 2m.
Pela conservação do momento linear, teremos:
Sendo a velocidade do centro de massa do haltere...
Passo 6
d)
Após a colisão, a rotação vai ser da seguinte forma:
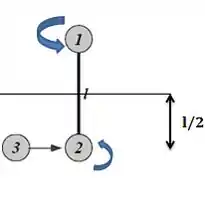
Como não tem nenhum torque agindo sobre o sistema, o momento angular é conservado. Daí, teremos:
Como e , vai ficar...
Passo 7
O nosso pode ser calculado por:
Resposta
d)