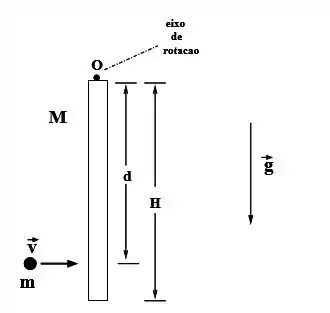
A figura mostra uma haste de massa e comprimento disposta verticalmente, e que se encontra inicialmente em repouso. A haste está pivotada na extremidade superior (ponto ) em torno da qual pode girar sem atrito. A haste é atingida a uma distância do ponto (conforme figura) por uma massa de modelar de massa que se desloca horizontalmente para a direita com velocidade escalar no momento da colisão. Após a colisão, a massa de modelar permanece grudada na haste. O momento de inércia da haste em relação ao seu centro de massa é . Considere que a massa de modelar pode ser tratada como uma partícula e .

(a) Qual é o momento de inércia do sistema (haste + massa) em relação ao eixo de rotação após a colisão?

(b) Qual é a velocidade angular ω do sistema, em função de , imediatamente após a colisão?

(c) Qual é a razão entre a energia cinética do sistema após a colisão e a energia cinética da massa de modelar imediatamente antes da colisão?

(d) Qual deve ser o valor de v para que o maior ângulo possível entre a haste e a vertical seja ?

(b) Usando a conservação do momento angular, temos que:

onde se refere ao momento angular do sistema imediatamente antes da colisão, e se refere ao momento angular do sistema imediatamente após a colisão, ambos medidos em relação ao ponto . Como apenas a massa de modelar possui velocidade antes da colisão, temos que . Após a colisão, a massa de modelar gruda na haste e o momento angular final é dado por . Igualando-se os momentos angulares inicial e final temos que:

e finalmente obtemos:

(c) A energia cinética inicial imediatamente antes da colisão corresponde à energia cinética da massa de modelar, . Já a energia cinética do sistema imediatamente após a colisão é igual a energia cinética de rotação do sistema, . Utilizando o resultado do item (a), obtemos que

Logo, a razão independe de .

(d) Assumindo que na posição do eixo de rotação, temos que imediatamente após a colisão a posição do centro de massa do sistema é dada por:

de forma que a variação da posição do centro de massa quando o ângulo entre a haste e a vertical é é igual a . Dado que a energia mecânica do sistema se conserva após a colisão, toda a energia cinética de rotação é transformada em energia potencial gravitacional do sistema, onde . Assim sendo,