Um bloco de massa , preso a uma corda ideal, se move em uma trajetória circular sobre uma mesa horizontal sem atrito. A corda é puxada para baixo lentamente, através de um buraco pequeno feito no meio do círculo, diminuindo assim o raio da órbita. É correto afirmar que:
(A) A energia cinética do bloco permanece constante.
(B) A energia cinética do bloco diminui com o tempo.
(C) O momento angular do bloco diminui com o tempo.
(D) O momento angular do bloco permanece constante.
(E) Tanto o momento angular do bloco quanto a sua energia cinética aumentam com o tempo.
Passo 1
Vamos dar uma olhada se a energia cinética e o momento angular variam.
Vamos começar com a energia cinética . Lembra daquele teorema trabalho energia cinética?
O trabalho resultante da força resultante sobre o corpo é igual a variação de sua energia cinética .
Nesse caso, até podemos pensar que a força de tração é perpendicular ao deslocamento devido à trajetória circular e por isso seu trabalho seria nulo:
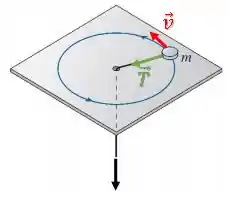
Porém o deslocamento só é realmente perpendicular à força quando o corpo faz uma trajetória circular sem alterar o raio .
Quando o fio vai sendo puxado, há uma componente radial do deslocamento na direção da força . Portanto, a força vai gerar um trabalho não nulo:
Logo, há variação da energia cinética do bloco.
Como o trabalho é positivo, a energia cinética do corpo aumenta.
Agora, vamos analisar o momento angular .
Podemos pensar no momento angular da partícula como:
Porém, tanto o raio quanto a velocidade variam conforme o fio é puxado, logo fica difícil analisar o momento angular assim.
Mas o momento angular só varia quando há um torque externo sendo aplicado no sistema:
A única força externa, além da força peso e normal (que se anulam), é a força de tração :
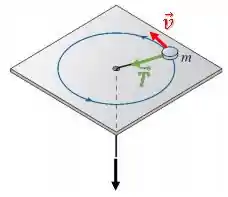
Essa força não gera torque na partícula com relação ao eixo de rotação passando pelo centro do círculo, pois ela esta na direção do eixo:
Como e são paralelos:
Como não há nenhum torque resultante sobre o sistema, temos que o momento angular não varia:
Como a derivada é zero, não varia:
Ficamos com a letra (D).
Resposta
Letra (D)