No sistema ao lado, um bloco de massa está unido por um fio de comprimento a um eixo em , e uma massa está unida à por um fio de comprimento (, , ). A massa dos fios é desprezível e o conjunto está apoiado sobre uma mesa horizontal sem atrito.
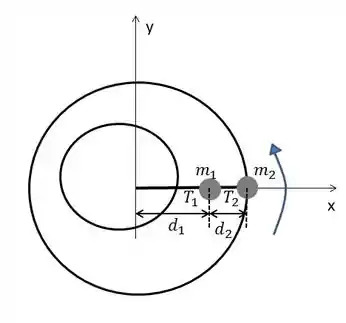
a) Sabendo que a corda que une à está sob uma tensão constante . Ache a velocidade angular constante do sistema, , e seu momento angular em relação ao ponto .
(dica: escreva a 2ª Lei de Newton para e discriminando com cuidado as tensões que agem sobre e )
b) Se o fio que liga a quebrar quando o sistema estiver passando sobre o eixo , descreva em poucas palavras o movimento subsequente de (fale sobre o tipo de movimento e a trajetória seguida e a velocidade do corpo).
c) Calcule o momento angular de após a ruptura do fio, , em relação ao ponto O.
Usando conservação de momento angular, calcule a velocidade angular final da massa ,
.
Passo 1
a)
Vamos lá. A questão ta pedindo pra gente calcular a velocidade angular e o momento angular em relação ao ponto . Ele dá uma dica, então vamos começar fazendo um diagrama de corpo livre para cada massinha, e ver quais são as forças atuando em cada uma:
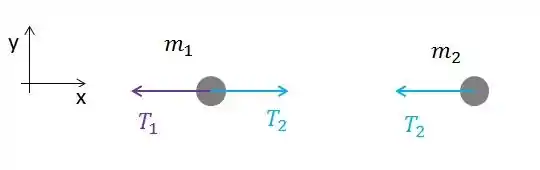
Não coloquei a normal e o peso porque estamos olhando por cima da mesa. A norma aponta pra cima da mesa, e o peso aponta pra baixo da mesa.
Para o corpo 1:
Para o corpo 2:
Outra coisa importante, é um movimento circular, certo? Então a aceleração é a aceleração centrípeta , apontando sempre para o centro da trajetória.
Onde esse R é o raio da trajetória circular. Pra massinha 1 é , pra massinha 2 é .
Usando a relação entre velocidade linear e angular:
Olha lá na figura do enunciado, se a aceleração aponta para o centro, temos que ela aponta para o sentido negativo de x.
Então a segunda lei de newton fica:
Para o corpo 1:
Para o corpo 2:
Agora é só brincar de substituir:
Substituindo a equação de no corpo 1:
Substituindo os valores:
Show!
Agora ainda temos que calcular o momento angular:
Passo 2
Sabemos que:
A velocidade angular a gente sabe. Só falta achar o momento de inércia.
Então vamos lá, como são partículas separadas é só somar o momento de cada uma em relação ao ponto :
Então:
Passo 3
(b)
Se o fio quebrar, não teremos mais a acelereção centrípeta.
Se estamos falando de um movimento sem aceleração, estamos falando de um movimento com a velocidade constate, logo é um movimento uniforme! A trajetória vai ser uma linha reta, e se o fio soltar quando o sistema estiver passando pelo eixo x, então é uma linha reta paralela ao eixo y.
Passo 4
(c)
Na ruptura, a velocidade é:
Assim,
Com não existem torques externos no sistema, o momento linear se conserva, então:
O momento angular inicial nos achamos lá na letra a:
Sabemos que
Show!!
Resposta
a)
b) Se o fio quebrar, não teremos mais a acelereção centrípeta.
Se estamos falando de um movimento sem aceleração, estamos falando de um movimento com a velocidade constate, logo é um movimento uniforme! A trajetória vai ser uma linha reta, e se o fio soltar quando o sistema estiver passando pelo eixo x, então é uma linha reta paralela ao eixo y.
c)