Uma patinadora passa a girar mais rápido ao fechar os seus braços, como ilustrado na figura abaixo.
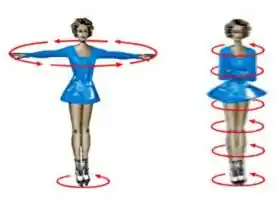
Isso ocorre porque:
(A) A patinadora sofre um torque externo que aumenta a sua aceleração angular.
(B) A energia rotacional da patinadora é conservada e, como o momento de inércia da patinadora diminui, a sua velocidade angular aumenta.
(C) O momento angular da patinadora é conservado e, como o momento de inércia da patinadora diminui, a sua velocidade angular aumenta.
(D) O centro de massa da patinadora muda e a variação de energia potencial gravitacional é convertida em rotação.
(E) Nenhuma das afirmações acima.
Passo 1
A patinadora ao longo de seu movimento de rotação não está sobre a ação de nenhuma força externa resultante, pois sua força peso e normal se anulam.
Como não há nenhuma força externa atuando, também não existe nenhum torque externo resultante sobre a patinadora.
Ma ué? Se nenhuma força atua sobre ela, como sua velocidade de rotação aumenta?
Ahhh, ai que está a questão...
Existe uma relação entre o torque resultante e o momento angular :
Sim, o torque é a variação do momento angular .
Se não há torque sobre o sistema, a variação do momento angular é nula, logo o momento angular da patinadora não se altera:
Opa, acho que temos algo por aí...
O momento angular pode ser escrito como:
Então, temos que:
Okay, mas e daí???
Ahh, é que quando a patinadora encolhe os braços e pernas, ela está aproximando sua massa do eixo de rotação e isso leva a uma diminuição de seu momento de inércia .
Então, se seu momento de inércia diminui, sua velocidade angular aumenta afim de compensar a igualdade do momento angular .
Apenas essa explicação está correta dentre as alternativas.
Ficamos com a letra (C).
Resposta
Letra (C)