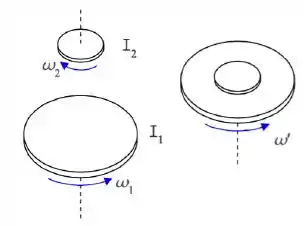
Um disco horizontal com momento de inércia em relação ao seu eixo de simetria, visto de cima, gira no sentido anti-horário com velocidade angular (valor absoluto). Um segundo disco, com momento de inércia em relação ao seu eixo de simetria, visto de cima, gira no sentido horário com velocidade angular (valor absoluto). Em um dado instante , o segundo disco é colocado em cima do primeiro, e os dois discos passam a girar juntos com uma certa velocidade angular em torno de um eixo de simetria comum. Nessa situação, a velocidade angular é:
(a)
(b)
(c)
(d)
(e)
Passo 1
Lembra de colisão entre duas partículas?
A força que a partícula 1 exercia sobre a partícula 2 era igual à força que a partícula 2 exercia na partícula 1 mas com o sentido oposto (ação e reação), logo, essas forças internas ao sistema se cancelavam.
Com isso, o sistema conservava o momento linear:
No caso dessa questão, temos algo parecido...
Quando os discos se encontram, o torque que o disco 1 exerce sobre o disco 2 é igual ao torque que o disco 2 exerce sobre o disco 1 mas com o sentido oposto (ação e reação), logo esses torques internos se cancelam.
Fazendo um paralelo com a colisão, se o sistema está livre de torques externos, o momento angular se conserva:
Então, o caminho da questão é calcular o momento angular desse sistema e, a partir disso, achar a velocidade angular final.
Passo 2
Na situação inicial, o momento angular do sistema será:
Momento angular é dado por:
Mas é uma grandeza vetorial, então precisamos prestar atenção ao sentido.
Se considerarmos que o giro no sentido anti-horário é positivo, temos:
Passo 3
Já na situação final, temos os dois discos girando junto, logo:
Passo 4
Vamos usar a conservação do momento angular do sistema e igualar as duas expressões achadas:
Resposta
Letra (a)