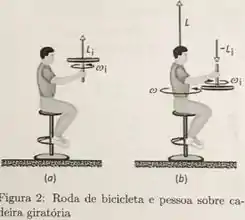
Uma pessoa sentada sobre uma cadeira giratória segura uma roda de bicicleta de momento de inércia , e que gira com velocidade angular inicial . De repente a pessoa inverte o sentido da roda da bicilceta conforme a figura 2, e isso faz com que o sistema total formado pela pessoa e a roda de bicicleta gire sobre o eixo da cadeira com velocidade angular final e momento angular da pessoa. Determine e o valore de se .
(A) e
(B) e
(C) e
(D) e
(E) e
Passo 1
Inicialmente, no sistema pessoa+roda, apenas a roda está em movimento.
Então, o momento angular inicial desse sistema é:
Passo 2
A jogada é que como não há nenhum torque externo sendo aplicado nesse sistema, o momento angular se conserva:
Ou seja, o momento angular final também será:
Passo 3
Mas como esse momento angular se conserva?
Quando ele inverte o sentido da roda, ela não pode simplesmente parar trocar o sentido de sua rotação...
Isso não acontece!
O que rola é que a roda mantem a sua rotação com a mesma velocidade angular . Porém agora, o sistema pessoa+roda entra em rotação para que o momento angular do sistema não se altere.
Então, temos dois momentos angulares, um em cada sentido:
Já achamos o momento angular da pessoa, agora podemos achar sua velocidade angular.
Passo 4
Substituindo os valores, temos:
Logo, ficamos com a letra (C).
Resposta
Letra (C)