Um disco pequeno de massa preso por um fio cuja outra extremidade está presa a um bloco de massa descreve um movimento circular uniforme de raio em uma mesa com um furo central por onde passa o fio. Sabe-se que a força de atrito entre o disco e a superfície da mesa é desprezível. Em um certo instante, uma força externa variável puxa o bloco de massa lentamente para baixo. A força externa, então, se estabiliza e observa-se que o disco passa a girar em torno do centro da mesa, em um movimento circular uniforme de raio .
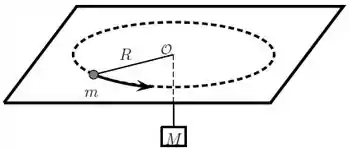
a) Qual o módulo da velocidade do disco durante o movimento circular inicial de raio ?
b) Qual passa a ser a velocidade angular de rotação quando o movimento circular passa a ter raio ?
c) Qual o trabalho realizado pela força externa que puxou o fio para que ocorra a mudança de movimento de circular de raio para o de raio ?
Passo 1
Inicialmente, o disco sobre a mesa realiza um MCU (movimento circular uniforme).
Para isso, a força resultante sobre o disco atua como força centrípeta.
E que força está fazendo esse papel de força centrípeta?
A força de tração no fio:
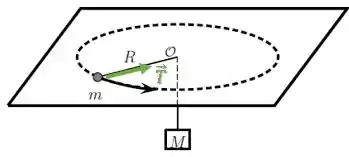
Passo 2
Podemos igualar essa força de tração à expressão da força centrípeta:
Mas não conhecemos ainda a força de tração ...
Passo 3
Então vamos aplicar a segunda lei de Newton ao bloco suspenso abaixo da mesa:
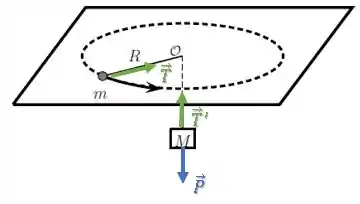
OBS: O vetor apresenta o mesmo módulo da força de tração , porém os vetores apontam em direções diferentes, por isso mudamos apenas seu nome.
Esse bloco está em equilíbrio!
Isso porque para que o disco realize um MCU, o raio da trajetória circular não muda, ou seja, o bloco não está subindo nem descendo abaixo da mesa.
Assim, temos que:
Passo 4
Agora podemos substituir o valor de na expressão da força centrípeta:
Isolando a velocidade, temos:
Passo 5
Agora na letra (b), uma força externa atua puxando o bloco para baixo.
Assim, o raio da trajetória do disco agora é .
Queremos saber a nova velocidade do disco sobre a mesa.
Poderíamos pensar em resolver exatamente da mesma maneira que o item anterior...
Porém, agora nós não conhecemos a força de tração, ou seja, não conhecemos o módulo da força centrípeta atuando sobre o disco.
Então, precisamos achar uma outra grandeza, de preferência que se conserve antes e depois dessa mudança.
Passo 6
Repara que a força de tração atua sempre perpendicular ao movimento do disco:
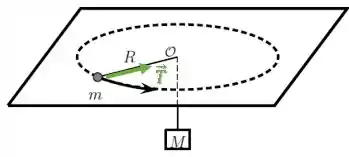
Assim, temos que essa força não gera torque com relação ao centro de rotação...
Se não tem nenhum torque atuando sobre o sistema, o Momento Angular se conserva:
A partir do momento angular conseguimos relacionar velocidade com o raio da trajetória circular.
Passo 7
O momento angular para uma partícula (disco) é dada pelo produto vetorial entre o vetor e o vetor momento linear :
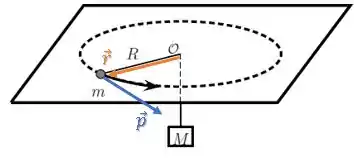
Como esses vetores são perpendiculares a todo instante, o módulo do produto vetorial fica:
O momento linear é dado pela massa vezes a velocidade:
Passo 8
Então, conservando o momento angular, temos:
O raio inicial é , enquanto no final passa a ser :
Cortanto e :
Substituindo a expressão que achamos na letra (a) para :
Passo 9
Porém, nós queremos a velocidade angular , então, vamos utilizar a relação:
Passando o para dentro da raiz elevado ao quadrado, ficamos com:
Passo 10
Já na letra (c), queremos o trabalho dessa força externa.
Bom, conhecemos o deslocamento radial do disco de ), entretanto, não conhecemos o módulo dessa força externa ao longo desse deslocamento.
Então, a melhor saída é aplicar o Teorema Trabalho-Energia Cinética que diz que:
Mas muito cuidado, essa força externa não é a única realizando trabalho.
Tanto a força peso do bloco quanto essa força externa atuam sobre a corda realizando trabalho:
Passo 11
O trabalho da força peso do bloco é:
Se o raio da trajetória do disco diminuiu , isso significa que o bloco desceu uma altura igual...
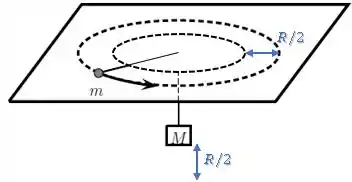
Substituindo isso no teorema, temos:
Passo 12
Vamos à variação da energia cinética .
Como temos apenas um movimento de rotação do disco, a energia cinética tanto inicial quanto num instante após a diminuição do raio será uma energia cinética de rotação:
O momento de inércia é do disco é calculado com:
Assim, temos que:
A velocidade angular final nós já encontramos no item (b):
Já a velocidade angular inicial , podemos descobrir a partir da velocidade :
Passando esse para dentro da raiz no denominador, ficamos com:
Passo 13
Substituindo e na variação de energia cinética:
Simplificando:
Passo 14
Voltando ao teorema, temos:
Pronto, achamos o trabalho da força externa, ufa!
Resposta
(a)
(b)
(c)