Tipler – Volume 1 – 6ª Ed. - Capítulo 9 – Seção 1 – Questão 72
(Capítulo 9.1 – Exercício 72) No sistema do problema 71, o bloco de é largado do repouso. (a) Determine a rapidez do bloco depois de ele ter caído uma distância de . (b) Qual é a rapidez angular da polia neste instante?
Passo 1
Eaeee gente, vamos lá?
Só pra lembrar, no exercício 71 tínhamos esse sistema:
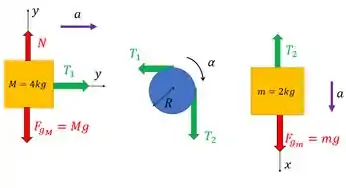
E aí o que rola agora é que esse bloco de massa vai ser largado a partir do repouso
Para encontrarmos as informações que o exercício pede, vamos usar conservação de energia ok? Vamos lá
Passo 2
a) A descida do bloco vai gerar um aumento de velocidade dos blocos e rotação da polia. Conservando a energia:
Então, encontramos a velocidade:
Passo 3
b) A velocidade angular vai vir daquela relação .
Então:
Sucesso?
Resposta
Exercícios de Livros Relacionados
Um homem está em pé em uma plataforma que gira (sem atrito) com uma velocidade angular de 1,2 r e v / s ; seus braços estão abertos e ele segura um tijolo em cada mão. O momento de inércia do sistema
Na figura abaixo duas partinadoras com 50kg de massa, que se movem com uma velocidade escalar de 1,4m/s , se aproximam em trajetórias paralelas separadas por 3m . Uma das patinadoras carrega uma vara
Um patinador girando. Podemos considerar as mãos e os braços esticados para fora de um patinador que se prepara para girar como uma barra delgada cujo eixo de giro passa pelo seu centro de gravidade (
Uma barra uniforme de 0,0300 kg e comprimento de 0,400 m gira em um plano horizontal em torno de um eixo fixo passando em seu centro e perpendicular à barra. Dois pequenos anéis, cada um com massa de
Um pequeno inseto de 10,0 g está pousado sobre uma das extremidades de uma barra delgada e uniforme, que está inicialmente em repouso sobre uma mesa horizontal lisa. A outra extremidade da barra pivot