Um astronauta está ligado a uma nave no espaço através de uma corda de de comprimento, que está completamente estendida inicialmente. Sem querer, ele aciona o seu dispositivo de propulsão, adquirindo uma velocidade tangencial de módulo e passando a descrever um movimento circular uniforme. Para tentar retornar à nave, ele começa a puxar a corda lentamente de maneira que a velocidade radial pode ser desconsiderada. Considere que, por ter uma massa muito maior que a do astronauta, a nave não se move e que a massa do astronauta com seu equipamento é de .
(a) Qual a velocidade tangencial do astronauta quando está a uma distância de da nave.
(b) Qual a força que o astronauta deve fazer sobre a corda para se manter a essa distância de da nave?
(c) Ao tentar se aproximar mais da nave, a corda não suporta a tensão e se rompe. Qual será o movimento seguido pelo astronauta após o rompimento da corda? Circular uniforme, retilíneo uniforme ou retilíneo uniformemente variado?
Passo 1
(a)
Vamos ver as forças que atuam no nosso sistema e analisar o movimento do astronauta:
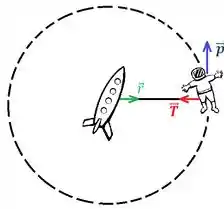
Nessas voltas e voltas que o coitado do astronauta está dando, a corda faz uma força sobre o astronauta que “aponta” sempre pro centro do movimento. Dá uma olhada no torque produzido por essa força:
Sempre que as forças apontarem pro centro, vamos considerar que o torque é nulo, beleza? E se não temos forças externas produzindo torque, o momento angular do astronauta é conservado!
Passo 2
Calcular a velocidade tangencial quando a distância do astronauta para a nave é de
Lembra que o momento angular é conservado? Molezinha agora. Pra responder a pergunta gente só precisa igualar os momentos angulares do nosso astronauta descuidado antes de puxar a corda e depois que ele ficou 60m de distância da nave:
Cortando a massa dos dois lados, ficamos com:
Passo 3
(b)
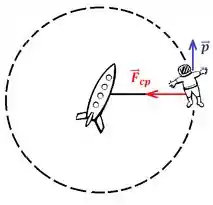
Nosso astronauta descuidado não estaria rodando sem a força que a corda exerce nele. Mas quem será essa força? Vamos descobrir?
Pra gente saber qual o tamanho dessa força, temos que saber primeiro quem é ela. Em movimentos circulares, temos sempre uma força que aponta pro centro, lembra? Isso mesmo, a força centrípeta! Como a tração é a única força que aponta pro centro, ela vai fazer o papel de força centrípeta. Agora é só calcular pessoal!
Passo 4
Vamos agora calcular a força centrípeta quando o astronauta está a da nave
Passo 5
(c)
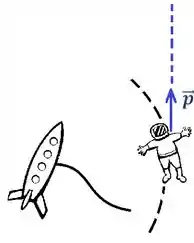
Quando a corda se rompe, o astronauta escapa pela tangente do movimento circular, realizando um movimento linear. O azarado vai ficar cada vez mais longe e não vai ter como voltar!
Como o coitado está no espaço, não há forças externas atuando sobre ele. Nosso astronauta então vai ficar perdido pra sempre no espaço, viajando a velocidade constante.
Resposta
b)
c) Movimento Retilíneo Uniforme