Um bloco de inércia é preso a um bloco de inércia por uma corda que passa por um disco uniforme de inércia e raio que pode rodar em torno do seu eixo. Inicialmente, o bloco de inércia é colocado de tal forma que a corda está tensionada. Ignore o atrito entre o disco e o eixo de rotação.
- Determine a aceleração angular da polia quando o sistema é liberado.
- Se o sistema é liberado a partir do repouso, qual é a velocidade do bloco de inércia após ele ter descido uma altura ?

Passo 1
POW! A aceleração angular pode ser retirada da informação do torque na polia...
Onde é o momento de inércia rotacional do disco com relação ao eixo de giro do centro. Pela teoria, para o disco de massa e raio ...
Então...
Mas para retirar a informação de ainda precisamos saber quem é o torque na polia.
Passo 2
Bem, pelo diagrama de corpos livres...
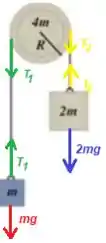
Bem, como a massa é mais pesada que a massa de um , a polia tende a girar para a direita, logo (embora não deu para desenhar isso no digrama de forças por que era um trechinho pequeno rsrs).
De acordo então com Newton, para cada bloco a resultante das forças (dado pela massa, vezes a aceleração do conjunto)...
POW! é maior que por estar levantando essa massa. Por outro lado, por esse bloco está descendo.
Passo 3
O torque resultante na polia pode então ser dado pela teoria (soma vetorial de todas as forças vezes o raio)...
Pela equação ...
E pela equação ...
De modo que...
Então, o torque rotacional será...
Passo 4
Retornando para a informação do torque no passo 1...
E substituindo...
Lembre-se de que a aceleração angular está relacionada com a aceleração normal por ...
Logo, a aceleração angular será...
Passo 5
POW! Podemos usar aqui a equação que relaciona velocidade e deslocamento : a equação de Torricelli:
Como o deslocamento é de () e o sistema parte do repouso ()...
A velocidade do bloco 2 então após descer a altura será...
Resposta
Letra A:
Letra B: