Uma pessoa está com os braços abertos sobre uma plataforma giratória (com atrito desprezível no giro) presa ao chão. Nessa posição, o momento de inércia da pessoa com a plataforma é em relação ao eixo de rotação da plataforma. Um disco uniforme de massa raio é lançado com velocidade e velocidade angular conforme a figura. O disco é agarrado pela mão e para de girar, ficando seu centro a uma distância do centro do sistema pessoa-plataforma, na altura dos braços. Determine:

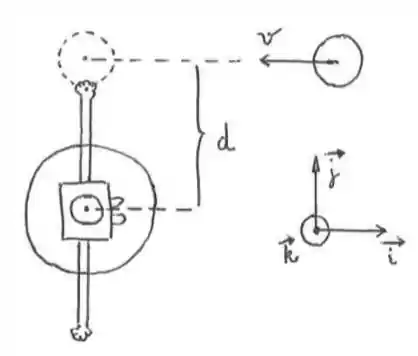
a) O vetor momento angular do disco em relação ao seu centro de massa antes de ser agarrado.

b) O vetor momento angular total do disco em relação ao centro do sistema pessoa-plataforma na altura dos braços, antes de ser agarrado.

c) O momento de inércia do conjunto plataforma-pessoa-disco em relação ao eixo de rotação da plataforma, após o disco ser agarrado.

d) Qual o vetor velocidade angular do conjunto plataforma-pessoa-disco após o disco ser agarrado pela mão? Girará o conjunto no sentido horário ou anti-horário?

b)

É bom tomar bastante cuidado com os vetores aqui!!

O momento angular nesse caso será dado pela soma do momento angular do centro de massa com a definição, é uma espécie de Teorema dos Eixos Paralelos para o momento angular, saca só:

Decompondo vetorialmente, teremos:

Daí...

O que nos dá como resposta...

c)

Sabemos que o será a soma dos momentos de inércia, logo:

Como o disco gira em torno de um eixo distante, pelo Teorema dos Eixos Paralelos, teremos:

d)

Não haverá torque pois a força resultante do sistema é o peso, que passa pelo eixo de rotação, logo o momento angular se conservará. Dessa forma, escrevemos:

Isolando o :

Que é o sentido anti-horário.