Um aro de raio e massa gira sem atrito, no plano horizontal em torno de um eixo vertical localizado no seu centro, com velocidade angular em relação a um observador fixo no solo. Esse aro está com quatro pequenas bolas, cada uma com massa e raio desprezível, fixadas na borda, a cada radianos. Vide figura.
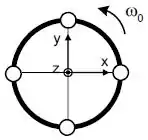
sendo: ; ; ;
a) Obtenha uma expressão literal, em termos dos dados fornecidos, para o momento angular inicial do sistema aro-quatro bolas, em relação à origem. Obtenha uma expressão literal para a energia cinética desse sistema.
Com relação aos dados do item anterior, admita que em um certo instante, duas daquelas bolas, situadas em extremidades opostas, sejam ejetadas por um mecanismo interno do aro, no mesmo sentido e direção das respectivas velocidades tangenciais dos pontos onde estão. Cada uma com velocidade de módulo igual a em relação ao mesmo observador externo.
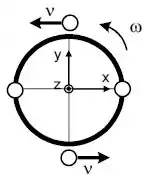
b) Encontre uma expressão literal em termos dos dados fornecidos para o módulo da nova velocidade angular do novo sistema aro-duas bolas. Explicite a lei física usada para obter os resultados.
Passo 1
Queremos o momento angular e a energia cinética desse sistema.
Vamos começar com o momento angular...
Podemos calcular o momento angular das partículas separadamente do aro e depois somarmos os dois. Entretanto, é mais prático calcular o momento angular desse sistema como um corpo só.
Momento angular de um corpo é dado por:
OBS: O corpo gira com no sentido anti-horário. Então pela regra da mão direita, nosso dedão fica para cima, logo a direção desse vetor é em positivo .
Assim, já sabemos a direção e o sentido do momento angular , que é a mesma de :
Passo 2
Vamos calcular o momento de inércia desse sistema, que achamos o momento angular.
O desse sistema será o momento de inercia do aro mais o momento de inércia das partículas. Como todas elas têm a mesma massa e estão a uma mesma distância do eixo, todas elas apresentam o mesmo momento de inércia :
O momento de inércia do aro é dado no formulário:
Substituindo a massa do disco e o raio , temos:
Já o momento de inércia de uma partícula é dado pela sua massa vezes o quadrado de sua distância :
Logo, temos:
Ou seja, o momento de inércia do conjunto será:
Substituindo esse valor, conseguimos o momento angular :
Passo 3
Já o momento de inércia também apresenta duas fórmulas, sendo uma para partículas e outra para corpos extensos.
Como já achamos o momento de inércia do sistema, vamos utilizar a seguinte expressão:
Então:
Passo 4
Na letra (b), temos que duas bolas foram ejetadas por um mecanismo interno com velocidade e queremos achar a nova velocidade angular do aro com as duas partículas restantes.
Um caminho para isso seria a partir da conservação do momento angular do sistema.
Porém, será que ele se conserva?
Bom, o mecanismo exerce uma força nas partícula, porém as partículas exercem a mesma força no sentido oposto sobre o mecanismo (ação e reação), elas são forças internas ao sistema aro-partículas.
Assim, os torques desses forças também serão internos ao sistema e se cancelam.
Resumindo, se não há torques externos sobre o sistema, o momento angular se conserva:
Passo 5
Já sabemo o momento angular inicial:
Vamos calcular o momento angular final . Ele será a soma do momento angular do aro com as duas partículas em rotação com o momento angular das duas partículas que foram lançadas .
Assim, a conservação fica:
Passo 6
será dado por:
Sendo o momento de inércia , o momento de inércia do disco mais duas partículas:
Logo:
Vamos para .
Os momentos angulares das partículas serão dados por:
Substituindo o valor de , temos:
Passo 7
Voltando a equação de conservação do momento angular, temos:
Podemos cortar e cortar :
Resposta
(a)
(b)