Considere o rotor de um helicóptero como sendo formado por três pás de comprimento e massa , unidas em suas extremidades (a largura e a espessura são desprezíveis em relação a). O eixo do rotor é perpendicular ao plano das pás (vide figura).
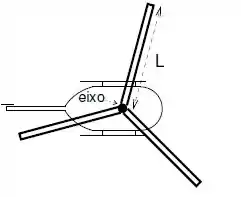
a) Calcule o momento de inércia de cada pá em relação ao eixo do rotor e o momento de inércia total do rotor.
b) Se e , calcule o torque necessário para que a velocidade angular do rotor varie uniformemente de zero a em segundos.
c) Qual a potência média transferida ao rotor nesse intervalo de tempo?
d) Considere que o momento de inércia da cabine do helicóptero em relação ao eixo do rotor seja de .Se não houvessem forças externas atuando sobre o conjunto cabine+rotor, qual seria a velocidade angular da cabine ao final do intervalo de tempo do item b?
Passo 1
a)
Bora lá! O momento de inércia a gente calcula pela formulitxa:
Colocando uma pá da hélice no eixo x e calculando nesse caso, substituiremos o r por x, certo?
Pra tudo ficar mais bonitinho, a gente pode fazer uma pequena alteração na integração. Do conceito de densidade linear, podemos dizer que , ou seja, e melhor ainda pra a gente .
Substituindo esse resultado na integral, teremos:
Ah, aí eu escrevi uma integral indefinida, mas na verdade sabemos os valores, o tamanho da pá vai da origem até o tamanho L, logo, reescrevendo a nossa integral, vai ficar:
Mas, como vimos, o nosso , ou melhor ainda, nesse caso em que o comprimento é e a massa é M, a gente vai escrever . Por último, substituindo no nosso ...
Passo 2
Para achar o momento inércia total basta multiplicar tudo por 3, já que o momento de inércia de várias partes nada mais é que a soma do momento de inércia em relação a um mesmo ponto. Logo:
Passo 3
b)
Molezinha!
Aqui é só lembrar a relação:
Então, vamos logo achar o valor numérico de já que já temos os valores de M e L.
E o nosso será nada mais nada menos que a nossa aceleração angular. Como o motor aumentou em em já temos o nosso também, certo?
Melhorando o nosso , ou melhor, passando para hertz, teremos:
E finalmente, para achar o nosso , podemos utilizar aquela formula da cinemática:
Agora é só jogar os valores mesmo!
Passo 4
c)
A potência a gente sabe que pode ser calculada por:
Nesse caso, o nosso tempo é 5s mesmo, então será: .
Passo 5
Mas na rotação com aceleração, quais são as variações de energia?
Somente a energia cinética de rotação, dada por:
Passo 6
d)
O enunciado faz questão de falar que não tem força externa agindo. Se não tem força externa, não tem torque, e assim o momento angular se conserva. Bora lá!
Como o helicóptero é dividido em Cabine e rotor, vamos fazer assim:
Como o helicóptero sai do repouso, . Daí vai sobrar:
Passo 7
Isolando o que é quem a gente quer calcular vai sobrar:
Agora é só substituir os valores e correr pro abraço!!