Calcule os limites:
e)
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu um limite e pediu pra gente calcular ele. Em outras palavras, ele quer saber o que acontece com a função quando tende a . Mas o quê que isso quer dizer?
Quer dizer que quanto mais vai se aproximando de , se esse limite existir, então a função vai se aproximando de um valor. E qual valor é esse?
É isso que nós vamos descobrir!
Passo 2
Vamos dar uma olhadinha no nosso limite:
Como é que a gente pode calcular o limite dessa função? Bom, se eu substituir o no lugar do , vai ficar assim:
Ou seja, temos uma indeterminação, que é uma expressão não sabemos exatamente como calcular. Beleza, então o que eu faço? Nós precisamos encontrar estratégias para fugir dessas indeterminações e transformar o nosso limite em algo simples de resolver.
Olhando para a nossa função, a gente percebe logo de cara que ela parece muito com um limite fundamental bem famoso, que é esse aqui:
Existem maneiras de demonstrar que esse limite é , uma delas é fazendo o cada vez menor e ir substituindo os valores ali, tipo assim:
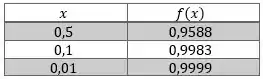
Percebe que quanto menor é o , mais a função vai se aproximando de ? Isso acontece também se a gente calcular para valores negativos. Então, nós podemos dizer que o limite dessa função é mesmo igual a . Tá, mas como isso me ajuda?
Como nossa função já é parecida com esse limite fundamental, o que a gente pode fazer é tornar ela ainda mais parecida pra conseguir associar o nosso limite a um resultado conhecido. Mas como é que eu posso fazer isso?
Passo 3
Bom, pra tornar nossa função mais parecida com aquele limite, a gente pode começar dividindo nossa função por em cima e embaixo:
Simplificando embaixo, nós temos:
Como temos uma divisão de frações, podemos escrever:
Lembra que quando a gente tem uma constante multiplicando no limite a gente passar ela pra o lado de fora do limite? Então, temos:
Agora olha só, nosso argumento na função seno é igual ao denominador, como na função .
E como , então o também é igual a , e temos:
Encontramos nosso resultado. Valeu, galera! 😉