Classifique os limites abaixo agora usando a noção generalizada que inclui ou como resposta.
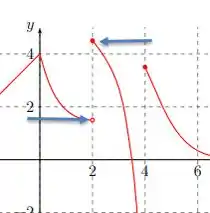
Em que é a função cujo gráfico é dado abaixo:
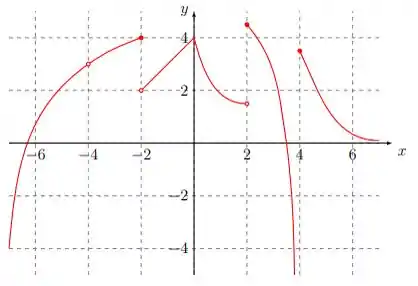
Passo 1
E ai galera, tudo bem?
Vou ajuda você aqui!
Primeiro vamos calcular
O gráfico em torno de é:
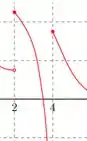
E quando nos aproximamos da função pelo lado esquerdo essa função vai lá pra baixo:
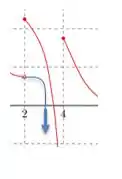
E lá pra baixo pra gente significa , então
Passo 2
Agora olhando a mesma região em torno de , mas vindo pela direita a unção é bem definida e tende a :
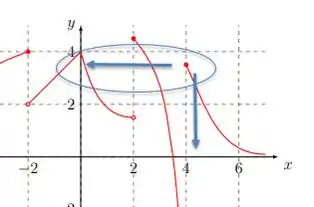
E é diferente do valor encontrado para o limite vindo pela esquerda. Assim os limites bilaterais são diferentes e o limite da função no ponto não existe:
Passo 3
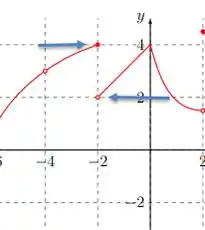
Agora o limite da função perto de também não existe, saca só:
Passo 4
E por fim em torno de também não existe limite:
Belezinha?
Espero ter ajudado!