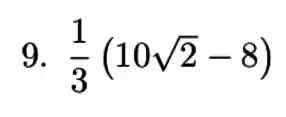
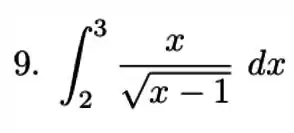
Passo 1
Pra resolver essa aqui, temos que fazer uma substituição. Vamos fazer
Passo 2
Agora vamos separar em duas integrais pra facilitar nossa vida
Passo 3
Beleza! Agora precisamos resolver as integrais separadamente
E
Passo 4
Antes de aplicar os limites de integração, temos que voltar para a forma original, substituindo e só depois substituir os valores
E
Passo 5
Por fim, só falta somar os valores que encontramos para as duas integrais.
Resposta
Exercícios de Livros Relacionados
Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 θ 6 sec 2 θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x