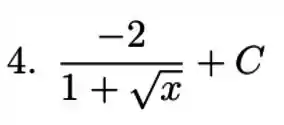
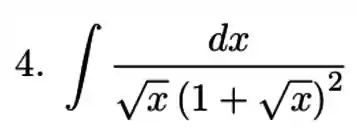
Passo 1
Você lembra que o truque da substituição simples é identificar dentro da integral uma parte que seja derivada da outra? Bom, veja que:
Então acho justo chamarmos:
Passo 2
Fazendo a substituição na integral:
Não se esqueça de olhar sua “nova” integral e verificar se ainda está presente nela: se estiver, volte porque errou a substituição, e se não estiver, parabéns e segue o baile!
Resolvendo a integral:
Passo 3
PASSO MUITO IMPORTANTE!
foi uma variável que VOCÊ criou. Agora temos que voltar pra variável do problema! Então ficaremos com:
Resposta
Exercícios de Livros Relacionados
Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 θ 6 sec 2 θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x