Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Simples

Ver Teoria
Exercício 114123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

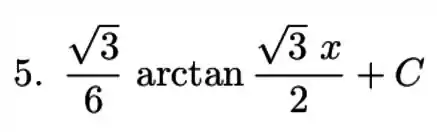
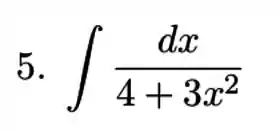
Passo 1

Cara, essa integral lembra muito algo relacionado ao a r c t a n ( x ) , mas tá um pouquinho diferente. Dá uma olhada de como devia ser:

∫ 1 1 + x 2 d x = a r c t a n x + C

Tá vendo como está super parecido? Bom, então vamos arrumar aquele denominador primeiro, ok?

∫ 1 4 + 3 x 2 d x = 1 4 ∫ 1 1 + 3 4 x 2 d x

Percebeu o porquê de fazer isto? Vamos chamar:

u 2 = 3 4 x 2 → u = 3 2 x → d u = 3 2 d x

2 3 d u = d x

Passo 2

Fazendo a substituição na integral:

1 4 ∫ 1 1 + 3 4 x 2 d x = 1 4 2 3 ∫ 1 1 + u 2 d u = 1 2 3 ∫ 1 1 + u 2 d u

Não se esqueça de olhar sua “nova” integral e verificar se x ainda está presente nela: se estiver, volte porque errou a substituição, e se não estiver, parabéns e segue o baile!

Resolvendo a integral:

1 2 3 ∫ 1 1 + u 2 d u = 1 2 3 a r c t a n u + C

Passo 3

PASSO MUITO IMPORTANTE!

u foi uma variável que VOCÊ criou. Agora temos que voltar pra variável do problema! Então ficaremos com:

u = 3 2 x

1 2 3 a r c t a n u + C = 3 6 a r c t a n 3 2 x + C

Perceba que a ideia neste exercício todo é você forçar aparecer aqueles termos que você já conhece a integral! Daí você manipula tudo e dá certo :)

Resposta

Exercícios de Livros Relacionados

Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos ⁡ 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 ⁡ θ 6 sec 2 ⁡ θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x