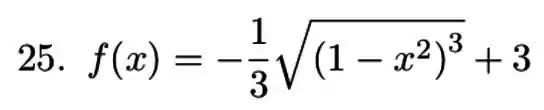Passo 1
Bom, o enunciado dá a expressão da derivada e pede a . Então precisamos integrar aquela derivada. Relaxa, que daqui a pouco a gente vai usar o ponto que ele deu.
Integrando ambos os lados com respeito a :
Passo 2
Vamos utilizar o método da substituição para resolver essa integral:
Passo 3
Substituindo na integral:
Passo 4
Resolvendo a integral:
Passo 5
Lembrando de algo MUITO IMPORTANTE! foi uma variável que você criou, então precisamos voltar para a variável do problema, ok?
Prontinho! Agora tá certinho. 😊
Passo 6
O que encontramos até agora foi uma família de funções que tem a derivada igual àquela dada no enunciado.
Finalmente, vamos usar aquela informação do ponto pertencer à função para descobrirmos o valor da constante .
Então a função procurada é:
Resposta
Exercícios de Livros Relacionados
Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 θ 6 sec 2 θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x