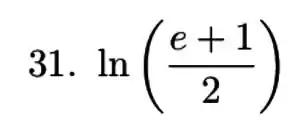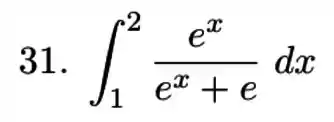
Passo 1
Bom, nessa questão vamos usar o método da substituição! Chamaremos:
O importante nesta questão é perceber que agora estamos tratando de integrais definidas. Então, se mudamos a variável, temos que mudar os limites de integração também.
Dado que , quando:
Passo 2
Substituindo na integral:
Passo 3
Resolvendo a integral:
Resposta
Exercícios de Livros Relacionados
Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 θ 6 sec 2 θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x