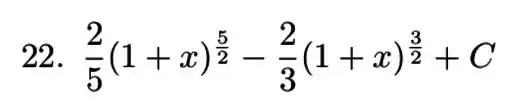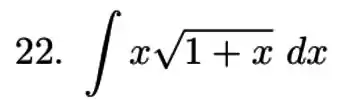
Passo 1
Precisamos determinar
Para isso podemos utilizar a substituição
Passo 2
Usando a substituição ficaremos com
Que podemos separar em
Passo 3
Resolvendo as integrais ficamos com
Desfazendo a substituição
Prontinho! Resolvida a nossa integral.
Resposta
Exercícios de Livros Relacionados
Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 θ 6 sec 2 θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x