Calcule:
f)
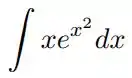
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinarmos o resultado da integral .
Para podermos resolver isso, podemos utilizar o método da substituição, onde e, portanto, .
Agora é só substituir!!
Não entendeu? Então bora junto 😉
Passo 2
Bom... dessa forma, aplicando a substituição, temos:
Entendeu direitinho? Responde aee ;)
