USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 2, Questão 5.3
Calcule o volume do sólido cuja base é a astróide de equação e tal que as seções transversais por planos paralelos ao plano são quadrados.
Passo 1
Eaee!!! Belezinha? Bom... a questão quer que a gente calcule o volume do sólido cuja base é a astróide de equação .
Lembrando que a figura da astróide é a seguinte:
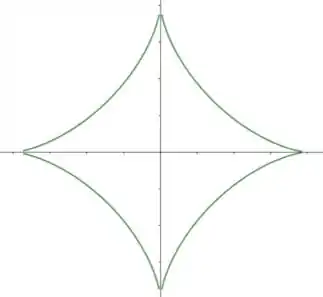
Além disso, a questão nos diz que as seções transversais por planos paralelos ao plano são quadrados.
Nesse sentido, como estamos trabalhando com seções transversais (planos) perpendiculares a um dos eixos coordenados, usamos a seguinte fórmula para o volume :
Onde é a área da base.
Agora vamos juntos!!
😉
Passo 2
Então... vamos primeiro reorganizar nossa equação da seguinte forma:
Assim, podemos calcular utilizando como base a área do quadrado:
Agora já podemos calcular nosso volume!!
Passo 3
Agora, podemos calcular parte do volume desse sólido apenas no primeiro octante e multiplicar por quatro, já que há uma simetria.
No entanto, não podemos esquecer também se o intervalo de varia de , e queremos calcular o volume somente no primeiro octante devemos multiplicar por dois e considerar os seguintes limites de integração .
Nesse sentido, temos:
Expandindo o cubo, obtemos:
Aplicando a regra da potência, resolvemos a integral:
Por fim, aplicando os limites de integração, temos:
Entendeu direitinho? Responde aee ;)
