Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Simples

Ver Teoria
Exercício 241234567891011121314151617181920212223252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Integração por Substituição

b Considere f : 0 , a → R contínua definida pelo gráfico abaixo e h : 0 , a 3 → R definida por h x = f 3 x . Mostre que A r e a A 1 = 3 A r e a A 2 .

( f i g u r a   r e t i r a d a   d a   p r o v a )

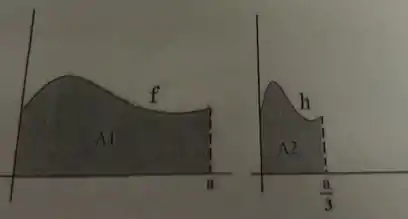
Passo 1

Vamos começar levando em conta o seguinte, pelos desenhos da figura:

∫ 0 a f x d x = A 1

∫ 0 a 3 h x d x = A 2

Sabemos ainda que o h x = f 3 x .

Digamos que a primitiva de f x é a função F x . Com isso, poderíamos dizer o seguinte:

∫ 0 a f x d x = F a - F 0 =   A 1

Ok, esse seria o processo de integração de f .

Passo 2

Agora, se a gente quisesse integrar a outra função, a h x = f 3 x ? Bom, nós poderíamos fazê-la com a ajuda de uma substituiçãozinha que simplifica muito:

∫ 0 a 3 h x d x = ∫ 0 a 3 f 3 x d x

u = 3 x → d u = 3 d x ;   d x = d u 3

x i n f = 0 → u i n f = 3 0 = 0

x s u p = a 3 → u i n f = 3 a 3 = a

Ou seja, ficamos com o seguinte:

∫ 0 a 3 f 3 x d x = ∫ 0 a f u d u 3

= F a - F 0 3 = A 1 3

Como a integral que fazemos gera a área A 2 , certificamos que:

A 2 = A 1 3

Resposta

A 2 = A 1 3

Exercícios de Livros Relacionados

Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos ⁡ 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 ⁡ θ 6 sec 2 ⁡ θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x