UnB - Cálculo I - Listas - Lista 13- Questão 2a
Calcule as integrais abaixo usando a Regra de Substituição, quando necessário.
Passo 1
Hellooo pessoal lindo do Responde Aí, tudo bem? Essa questão parece complicada, mas vou ajudar você aqui! Vamos começar?
A primeira coisa que podemos notar dessa questão é que a nossa integral é definida, uma vez que ela possui limites de integração. Além disso, agora sabemos também que por ser uma integral definida a resposta será um número e não mais uma outra função.
Bom, a questão quer saber qual será , ademais o enunciado da questão ainda nos dá uma dica fundamental que é o fato de podermos utilizar a Regra da Substituição sempre que julgarmos necessário. Como poderemos dar início???
Passo 2
Iremos utilizar a Regra da Substituição, a regra da substituição consiste em fazer uma mudança de variável com o objetivo de otimizar os cálculos. Chamaremos . Calculando a derivada
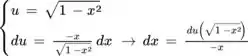
Reescrevendo a expressão temos que
Passo 3
Substituindo na equação do passo anterior por encontramos que
Bons Estudos! Beijinhos :)