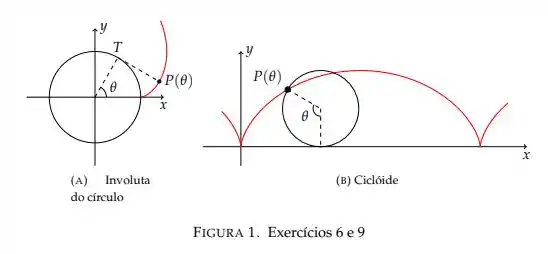
Uma circunferência de raio rola sem escorregar ao longo do eixo . Encontre equações paramétricas para a curva descrita por um ponto da circunferência que se encontra inicialmente na origem. (Esta curva é chamada ciclóide, veja a Figura 1(b))
Passo 1
Eaew, beleza?
Temos uma circunferência de raio rolando ao longo do eixo (para a direita), precisamos parametrizar a curva que o ponto percorre enquanto este movimento ocorre, esta curva é o ciclóide descrito na parte da figura
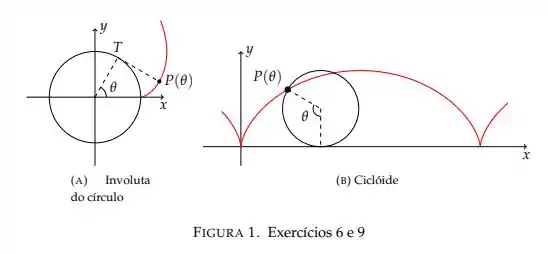
O segredo aqui é escrever as coordenadas e em termos de e , mas para fazer isso será necessário usar algumas relações trigonométricas básicas e visualizar algumas figuras! Vem comigo!
Passo 2
Imagine que essa roda está molhada de tinta e que por onde passa ela deixa um rastro! O tamanho do rastro será exatamente o tamanho do arco que tocou o chão ao longo do movimento, então, temos que a seguinte distância
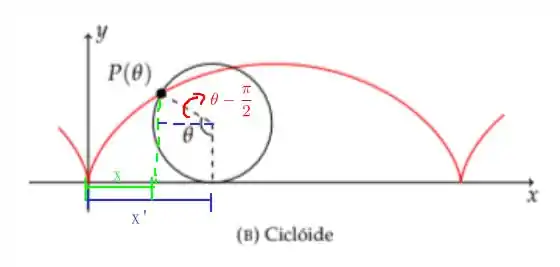
em que temos que , comprimento de arco, mas note que a coordenada no ponto será
já que o cosseno e o seno são duas funções trigonométricas relacionadas por uma fase . Da mesma forma, temos que a coordenada vertical será
em que o sinal de menos surge devido a paridade da função seno! Se quiser visualizar isso um pouco melhor tente expandir a expressão e usando a identidade trigonométrica, a parametrização do ciclóide é então dada por
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta