Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Simples

Ver Teoria
Exercício 375123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UnB – Cálculo I – Lista 17 – 20h

Calcule a integral.

∫ 1 + x 2 x d x

Passo 1

O triângulo retângulo associado a esse desenho é o seguinte:

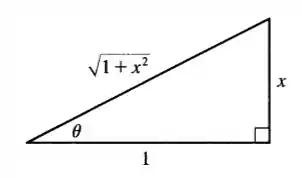
Passo 2

A gente tem que x = tg ⁡ θ , e θ varia no intervalos - π 2 ≤ θ ≤ π 2 . Assim, se fizermos a derivada de x , a gente tem d x = sec 2 ⁡ θ d θ .

Agora, achando o valor da nossa hipotenusa x 2 + 1 por meio da substituição de x , temos:

x 2 + 1 = sec ⁡ θ

Passo 3

Assim, o valor da nossa integral é:

∫ 1 + x 2 x d x = ∫ sec ⁡ θ tg ⁡ θ sec 2 ⁡ θ d θ = ∫ sec ⁡ θ tg ⁡ θ 1 + tg 2 ⁡ θ d θ = ∫ ( csc ⁡ θ + sec ⁡ θ tg ⁡ θ )   d θ

= - ln ⁡ csc ⁡ θ + cot ⁡ θ + sec ⁡ θ + C = - ln ⁡ 1 + x 2 x + 1 x + 1 + x 2 1 + C

= - ln ⁡ 1 + x 2 + 1 x + 1 + x 2 + C    

Resposta

∫ 1 + x 2 x d x = - ln ⁡ 1 + x 2 + 1 x + 1 + x 2 + C    

Exercícios de Livros Relacionados

Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos ⁡ 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 ⁡ θ 6 sec 2 ⁡ θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x