Calcule as seguintes primitivas:
Passo 1
Bom dia, boa tarde e boa noiteeee! Xuxus, essa questão é um pouco mais complicadinha, mas, eu vou te ajudar a tornar tudo mais fácil. Bora!
Temos que calcular a função primitiva da integral . Tá mais o que é essa primitiva??
Bom, quando temos uma integral indefinida o seu resultado é representado por uma função que chamamos de “primitiva” e não por um valor numérico.
Onde,
: É uma função conhecida, nessa questão é ;
: É a primitiva de ;
Então nessa questão devemos justamente encontrar a nossa função primitiva correspondente. Tranquilinho?! E como poderemos encontrar essa função??
Passo 2
Galera, essa questão é uma viagem hahaha! Porque vamos ter que utilizar a técnica de substituição para facilitar nossos cálculos, mas, nós temos que encontrar uma maneira de relacionar a raiz com o . E a viagem se encontra no fato desses valores serem as medidas dos lados de um triângulo retângulo.
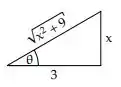
Sim, eu sei! É difícil pensar nisso, essa é uma das sacadas que deixam a questão bem complicada.
Bom, avaliando o triângulo temos que:
Derivando esse , porque precisamos substituir o por alguma expressão:
E como queremos também trocar aquela raiz feia ali por algo mais fácil de trabalhar. Bora fazer umas manipulações matemáticas.
E como :
Então pessoal , essa conta toda foi para conseguirmos substituir os termos da nossa integral, vamos montar essa com essa nova roupagem.
Passo 3
Substituindo os termos da nossa integral,
E como as funções tangente e secante são determinadas a partir do cosseno e seno, vamos passar nossa expressão para essas funções mais básicas.
Lembrando que
Então,
E a partir da equação trigonométrica fundamental conseguiremos substituir a função seno e passaremos a trabalhar apenas com a função cosseno.
Multiplicando ambos por , uma vez que precisamos do valor de .
Agora, voltemos para a nossa expressão da integral. Substituindo por . Temos o seguinte,
Passo 4
Vamos ter que utilizar novamente o método da substituição para conseguirmos prosseguir em nossa questão.
Logo,
Então,
Portanto, a nossa integral vai mudar de cara novamente. Pessoal, entendo que esteja um tanto cansativo esse problema. No entanto, juro que é para facilitar os cálculos hahaha.
Substituindo os termos por :
Agora vamos aplicar uma propriedade das integrais para a subtração de funções. Já que
Dessa forma,
Utilizando o seguinte macete para encontrar o valor das integrais para funções polinomiais:
Encontramos que a integral acima terá o seguinte valor:
Passo 5
Bom, utilizamos a regra da substituição algumas vezes nesse problema sendo assim é preciso voltar para a variável que tínhamos no início de tudo.
Como,
E
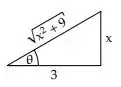
Podemos concluir que
Basta então, substituímos esse valor de no resultado da integral que obtemos no passo anterior.
Passo 6
Por fim, colocando em evidência. Obtemos um resultado mais agradável.
E até que fim, encontramos o nosso resultado. Então o que eu quero que vocês tirem dessa questão é resolver integrais indefinidas e a pensar fora da caixinha na hora de tentar resolver. Porque às vezes sabemos aplicar todos os métodos de resolução, entretanto, não conseguimos enxergar de maneira tão simples algumas substituições.
Então, é isso! Se cuidem e bons estudos ☺