Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Simples

Ver Teoria
Exercício 171123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UnB. Cálculo 1. Prova P3. 2021.1. Questão 2.

Deseja-se calcular a área sob o gráfico da função f ( x ) = x 4 - x 2 para 0 ≤ x ≤ 1 .

a) Explique, por meio de um teorema, por que utilizamos uma primitiva da função para o cálculo da área sob seu gráfico.

b) Utilize a substituição u = 4 - x 2 e reescreva a integral ∫ 0 1 f ( x ) d x apenas em termos da variável u .

c) Utilize a substituição x = 2 s e n ( θ ) e reescreva a integral ∫ 0 1 f ( x ) d x apenas em termos da variável θ .

d) Escolha um dos itens acima para determinar a área desejada.

Passo 1

Iae, meus queridos! Tudo certinho??

Bastante interessante, essa questão, foi dado uma função f x e temos que calcular a área sobre essa função dentro do intervalo 0 ≤ x ≤ 1 .

No item a), temos que usar um teorema para explicar por que utilizamos a primitiva da função para o cálculo da área sob seu gráfico.

Podemos dizer que de acordo com o teorema fundamental do cálculo, a integral de uma função representa a área contida abaixo da função.

Por exemplo, no nosso caso a integral da nossa f x com o intervalo de integração de x variando de 0 a 1 vai nos resultar a área abaixo da função neste intervalo.

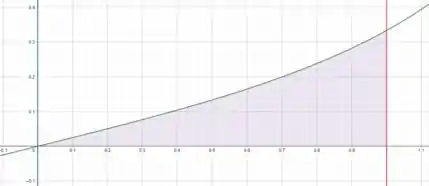
Como vemos na área roxa do gráfico de f x

Passo 2

No item b), se usarmos u = 4 - x 2 , vamos ter d u = - 2 x → x = d u / - 2 d x .

Temos que ajustar também nosso intervalo de integração, se 0 ≤ x ≤ 1 , substituindo em u vamos ter

p a r a   x = 0 ;   u = 4 - 0 ,   u = 4

p a r a   x = 1 ; u = 4 - 1 2 ,   u = 3

Então nossa integral será

∫ 0 1 x 4 - x 2 d x → ∫ 4 - 0 4 - 1 2 d u / - 2 d x u d x → ∫ 4 3 - 1 2 u d u

Podemos inverter os limites de integração para tirar esse sinal negativo da integral

∫ 3 4 1 2 u d u

Passo 3

No item c), vamos considerar x = 2 s e n θ e escrever nossa integral com relação a θ .

Com isso, temos que ajustar nossa função

f x = x 4 - x 2 → f θ = 2 s e n θ 4 - 2 s e n θ 2

f θ = 2 s e n θ 4 - 2 s e n θ 2 → f θ = 2 s e n θ 4 - 4 s e n ² θ

Temos uma simplificação que vamos aplicar que vai facilitar muito nossa vida, que é

s e n 2 θ + c o s 2 θ = 1

Multiplicando os dois lados por 4 , temos

4 s e n 2 θ + 4 c o s 2 θ = 4

Manipulando essa equação, temos

4 c o s 2 θ = 4 - 4 s e n 2 θ

Ou seja, 4 c o s 2 θ é igual nosso denominador da função f θ , assim podemos substitui-lo

f θ = 2 s e n θ 4 - 4 s e n ² θ → f θ = 2 s e n θ 4 c o s 2 θ = f θ = 1 2 · s e n θ c o s 2 θ

Ou seja, nossa nova função será

f θ = 1 2 · s e n θ c o s 2 θ

Nosso intervalo de integração será

s e   x = 0 ,   0 = 2 s e n θ → s e n θ = 0 → θ = 0

s e   x = 1 ,   1 = 2 s e n θ → s e n θ = 1 2 → θ = π 6

Vamos montar nossa integral. Se considerarmos u = cos ⁡ θ , nosso d u = - s e n θ

Com isso, nossos limites de u será

s e   θ = 0 ,   u = cos ⁡ 0 → u = 1

s e   θ = π 6 ,   u = cos ⁡ π 6 → u = 3 2

Ou seja, essa mudança facilitou muito já que nossa integral será

1 2 ∫ 3 2 1 - 1 u 2 d u   o u   1 2 ∫ 1 3 2 1 u 2 d u

Passo 4

Por fim, vamos escolher uma das integrais para resolvermos, mas por descargo de consciência, vamos resolver as duas integrais.

A primeira, quando u = 4 - x 2 , temos

∫ 3 4 1 2 u d u = 1 2 ln ⁡ u ​ 3 4

∫ 3 4 1 2 u d u = 1 2 ln ⁡ 4 - ln ⁡ 3 ≅ 0,1438

Para a segunda, quando u = cos ⁡ θ , temos

1 2 ∫ 1 3 2 - 1 u 2 d u = 1 2 1 u ​ 1 3 2

1 2 ∫ 1 3 2 - 1 u 2 d u = 1 2 1 3 2 - 1 ≅ 0,0773

É isso! Entendeu tudo? Responde Aí! 😎👍

Resposta

a) explicação no passo-a-passo

b) ∫ 3 4 1 2 u d u

c) 1 2 ∫ 1 3 2 1 u 2 d u

d) 0,1438 ou 0,0773

Exercícios de Livros Relacionados

Calcule a integral.int x^3 (x - 1)^(- 4) d x
Calcule a integral fazendo a substituição dada. ∫ cos ⁡ 3 x d x , u = 3 x
32. int (d t)/((2 + t)^2)
Use a fórmula de substituição do Teorema 7 para calcular as integrais nos Exercícios 1-46. ∫ π 3 π / 2 cot 5 ⁡ θ 6 sec 2 ⁡ θ 6 d θ
Calcule a integralint (sec x cos 2 x)/(s e n x + sec x) d x