Integrais indefinidas, o TVT e Regra de substituição - UFRJ
Encontre a integral indefinida
g.
Passo 1
Faaala galerinha 😊, nesse exercício vamos estudar a Técnica da Substituição para integrais simples.
De início essa técnica pode parecer um pouco confusa, mas aqui iremos torna-la descomplicada.
Essa técnica é indicada para integrais que estejam na seguinte forma
Ou seja, dentro da integral existe uma função e também a sua derivada.
Aqui nós substituímos g(x) pela variável u, e obtemos o diferencial de u (du) da seguinte forma
Logo
Onde F(x) é a função primitiva. E, claro, não esqueceremos de botar a constante C ao final da expressão para indicar que a primitiva está na sua forma generalizada e que C pode ser qualquer valor real.
Para deixar mais claro como devemos usar essa técnica vamos resolver a questão.
Passo 2
Vamos para a integral
Aqui, precisaremos usar um pouco mais a imaginação e visualizarmos o seguinte triângulo
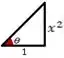
Com essa imagem, podemos assumir que . Logo,
Passo 3
Agora, fazemos nossa substituição dentro da integral. Assim,
Aqui temos uma integral que aparenta ser complicada. Mas ela se torna muito mais simples se usarmos a identidade trigonométrica fundamental, em uma versão diferente, que é
Logo,
Passo 4
Por fim, retornamos à nossa variável original x. Logo,
E,
Pronto!! Técnica da substituição aplicada com sucesso, com simplicidade e um pouco de criatividade. Poje é isso pessoal, até a próxima😁😉
Resposta
c.