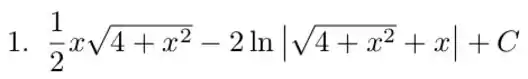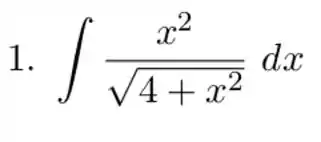
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 130123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Nosso primeiro passo é identificar qual nosso caso de substituição trigonométrica precisamos usar.

Perceba que temos

4 + x 2

Que está no mesmo formato que

a 2 + x 2

Nesse caso

x = a tan ⁡ θ

Então teremos

x = 2 tan ⁡ θ

Passo 2

A próxima coisa a se fazer é encontrar d x , derivando

x = 2 tan ⁡ θ

d x = 2 sec 2 ⁡ θ   d θ

Passo 3

Agora precisamos substituir x e d x na nossa integral

∫ x 2 4 + x 2 d x = ∫ 4 tan 2 ⁡ θ 4 + 4 tan 2 ⁡ θ 2 sec 2 ⁡ θ d θ

∫ x 2 4 + x 2 d x = 4 ∫ tan 2 ⁡ θ 4 ( 1 + tan 2 ⁡ θ ) 2 sec 2 ⁡ θ d θ

Substituindo tan 2 ⁡ θ + 1 = sec 2 ⁡ θ

∫ x 2 4 + x 2 d x = 4 ∫ tan 2 ⁡ θ 4 sec 2 ⁡ θ 2 sec 2 ⁡ θ d θ

∫ x 2 4 + x 2 d x = 4 ∫ tan 2 ⁡ θ 2 sec ⁡ θ 2 sec 2 ⁡ θ d θ

∫ x 2 4 + x 2 d x = 4 ∫ tan 2 ⁡ θ sec ⁡ θ d θ

Fazendo novamente a mesma substituição

∫ x 2 4 + x 2 d x = 4 ∫ ( sec 2 ⁡ θ - 1 )  sec ⁡ θ d θ

Então podemos dividir o problema em duas integrais

∫ x 2 4 + x 2 d x = 4 ∫ sec 3 ⁡ θ   d θ - 4 ∫ sec ⁡ θ d θ

Passo 4

O próximo passo é resolver mesmo nossa integral, vamos começar por

∫ sec 3 ⁡ θ   d θ = ∫ sec 2 ⁡ θ sec ⁡ θ d θ

Vamos resolver por partes

u = sec ⁡ θ

d u = sec ⁡ θ tan ⁡ θ   d θ

d v = sec 2 ⁡ θ

v = tan ⁡ θ

Utilizando a formula da integral por partes

∫ sec 3 ⁡ θ   d θ = sec ⁡ θ tan ⁡ θ - ∫ tan 2 ⁡ θ sec ⁡ θ d θ

Fazendo a substituição tan 2 ⁡ θ = sec 2 ⁡ θ - 1

∫ sec 3 ⁡ θ   d θ = sec ⁡ θ tan ⁡ θ - ∫ sec 3 ⁡ θ d θ + ∫ sec ⁡ θ d θ

∫ sec 3 ⁡ θ   d θ = 1 2 sec ⁡ θ tan ⁡ θ + 1 2 ∫ sec ⁡ θ d θ

Então, se voltarmos para nossa expressão

∫ x 2 4 + x 2 d x = 4 ∫ sec 3 ⁡ θ   d θ - 4 ∫ sec ⁡ θ d θ

∫ x 2 4 + x 2 d x = 4 1 2 sec ⁡ θ tan ⁡ θ + 1 2 ∫ sec ⁡ θ d θ - 4 ∫ sec ⁡ θ d θ

∫ x 2 4 + x 2 d x = 2 sec ⁡ θ tan ⁡ θ - 2 ∫ sec ⁡ θ d θ

Por fim

∫ x 2 4 + x 2 d x = 2 sec ⁡ θ tan ⁡ θ - 2 ln ⁡ sec ⁡ θ + tan ⁡ θ + C

Passo 5

Mas não podemos dar a resposta em função de θ , precisamos voltar para x . Para isso vamos precisar do triângulo retângulo.

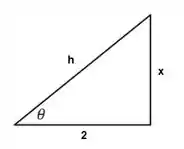
tan ⁡ θ = c a t e t o   o p o s t o c a t e t o   a d j a c e n t e = x 2

Usando Pitágoras podemos encontrar a hipotenusa

h 2 = 2 2 + x 2

h = 4 + x 2

Então

sec ⁡ θ = 4 + x 2 2

Vamos substituir então na nossa integral

∫ x 2 4 + x 2 d x = 2 sec ⁡ θ tan ⁡ θ - 2 ln ⁡ sec ⁡ θ + tan ⁡ θ + C

∫ x 2 4 + x 2 d x = 2 4 + x 2 2 x 2 - 2 ln ⁡ 4 + x 2 2 + x 2 + C

∫ x 2 4 + x 2 d x = 2 4 + x 2 2 x 2 - 2 ln ⁡ 4 + x 2 + x 2 + C

Usando as propriedades de log:

∫ x 2 4 + x 2 d x = 2 4 + x 2 2 x 2 - 2 ( ln ⁡ 4 + x 2 + x - ln ⁡ 2 + C

Mas ln ⁡ 2   é constante também, certo? Então podemos incorporar ele no C .

∫ x 2 4 + x 2 d x = x 2 4 + x 2 - 2 ln ⁡ 4 + x 2 + x + C

Finalmente!

Resposta

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x