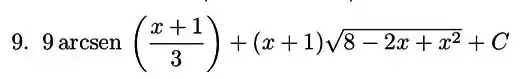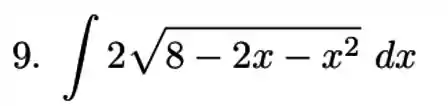
Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 182123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Passo 1

Inicialmente, precisamos encontrar qual caso de substituição se aplica na nossa integral

∫ 2 8 - 2 x - x 2 d x = 2 ∫ 9 - 1 - 2 x - x 2 d x

∫ 2 8 - 2 x - x 2 d x = 2 ∫ 9 - x + 1 2 d x

Para facilitar nossa vida vamos fazer uma substituição

u = x + 1

d u = d x

Então

∫ 2 8 - 2 x - x 2 d x = 2 ∫ 9 - u 2 d u

Repare que está no mesmo formato de

a 2 - u 2

Nesse caso

u = a sen ⁡ θ

Então teremos

u = 3 sen ⁡ θ

Passo 2

A próxima coisa a se fazer é encontrar d u , derivando

u = 3 sen ⁡ θ

d u = 3 cos ⁡ θ d θ

Passo 3

Agora precisamos substituir u   e d u na nossa integral.

∫ 2 8 - 2 x - x 2 d x = 2 ∫ 9 - 9 sen 2 ⁡ θ 3 cos ⁡ θ d θ

∫ 2 8 - 2 x - x 2 d x = 6 ∫ 9 ( 1 - sen 2 ⁡ θ ) cos ⁡ θ d θ

Vamos fazer a substituição cos 2 ⁡ θ = 1 - sen 2 ⁡ θ

∫ 2 8 - 2 x - x 2 d x = 6 ∫ 9 cos 2 ⁡ θ cos ⁡ θ d θ

∫ 2 8 - 2 x - x 2 d x = 18 ∫ cos 2 ⁡ θ d θ

Por fim, vamos usar mais uma identidade trigonométrica

cos 2 ⁡ θ = 1 - cos ⁡ 2 θ 2

∫ 2 8 - 2 x - x 2 d x = 18 ∫ 1 + cos ⁡ 2 θ 2 d θ

∫ 2 8 - 2 x - x 2 d x = 9 ∫ d θ + 9 ∫ cos ⁡ ( 2 θ ) d θ

Passo 4

O próximo passo é resolver a integral

∫ 2 8 - 2 x - x 2 d x = 9 ∫ d θ + 9 ∫ cos ⁡ ( 2 θ ) d θ

∫ 2 8 - 2 x - x 2 d x = 9 θ + 9 sen ⁡ θ cos ⁡ θ

Passo 5

Mas não podemos dar a resposta em função de θ , precisamos voltar para u e depois para x . Para isso vamos precisar do triângulo retângulo. Sabemos que

sen ⁡ θ = u 3

Então

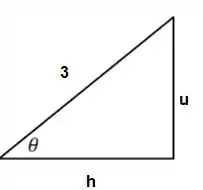
Usando Pitágoras podemos encontrar o cateto adjacente

9 = h 2 + u 2

h = 9 - u 2

Com isso, encontramos

sen ⁡ θ = u 3

cos ⁡ θ = 9 - u 2 3

E

θ = arcsen ⁡ u 3

Substituindo na nossa integral

∫ 2 8 - 2 x - x 2 d x = 9 arcsen ⁡ u 3 + 9 u 3 9 - u 2 3

∫ 2 8 - 2 x - x 2 d x = 9 arcsen ⁡ u 3 + u 9 - u 2

Passo 6

Tá quase acabando! Vamos agora só substituir u = x + 1 , que foi a substituição que fizemos lá no início.

∫ 2 8 - 2 x - x 2 d x = 9 arcsen ⁡ u 3 + u 9 - u 2

∫ 2 8 - 2 x - x 2 d x = 9 arcsen ⁡ x + 1 3 + ( x + 1 ) 9 - x + 1 2

∫ 2 8 - 2 x - x 2 d x = 9 arcsen ⁡ x + 1 3 + x + 1 8 - 2 x - x 2 + C

Fim! Cuidado para não esquecer a constante de integração.

Resposta

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x