Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 152123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

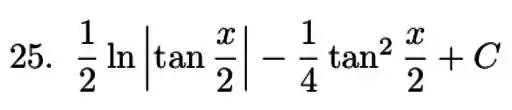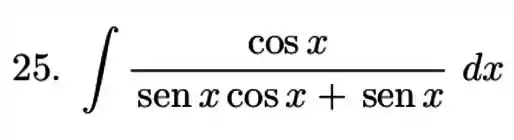
Passo 1

Vamos resolver utilizando o método da substituição de

z = tan ⁡ x 2

cos ⁡ x = 1 - z 2 1 + z 2

sen ⁡ x = 2 z 1 + z 2

E

d x = 2 d z 1 + z 2

Passo 2

Temos

∫ cos ⁡ x sen ⁡ x cos ⁡ x + sen ⁡ x d x = ∫ cos ⁡ x sen ⁡ x cos ⁡ x + 1 d x

Substituindo na nossa integral vamos ficar com

∫ cos ⁡ x sen ⁡ x cos ⁡ x + 1 d x = ∫ 1 - z 2 1 + z 2 2 z 1 + z 2 1 - z 2 1 + z 2 + 1 2 d z 1 + z 2

Simplificando temos

∫ cos ⁡ x sen ⁡ x cos ⁡ x + 1 d x = ∫ 1 - z 2 1 + z 2 z 1 - z 2 1 + z 2 + 1 + z 2 1 + z 2 d z

∫ cos ⁡ x sen ⁡ x cos ⁡ x + 1 d x = ∫ 1 - z 2 1 + z 2 z 2 1 + z 2 d z

∫ cos ⁡ x sen ⁡ x cos ⁡ x + 1 d x = ∫ 1 - z 2 2 z d z

Passo 3

Agora podemos separar em duas integrais

∫ cos ⁡ x sen ⁡ x cos ⁡ x + 1 d x = ∫ 1 - z 2 2 z d z

∫ cos ⁡ x sen ⁡ x cos ⁡ x + 1 d x = 1 2 ∫ 1 z d z - 1 2 ∫ z   d z

Integrando ficamos com

∫ cos ⁡ x sen ⁡ x cos ⁡ x + 1 d x = 1 2 ln ⁡ z - 1 4 z 2 + C

Passo 4

Desfazendo a substituição z = tan ⁡ x 2

∫ cos ⁡ x sen ⁡ x cos ⁡ x + 1 d x = 1 2 ln ⁡ tan ⁡ x 2 - 1 4 tan 2 ⁡ x 2 + C

Resolvido!

Resposta

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x