Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 151123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

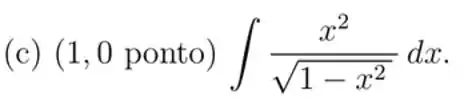
Passo 1

Aqui nós temos que usar a substituição trigonométrica esse é o caso da substituição do seno:

1 - x 2 = a 2 - x 2   →       x = a sen ⁡ θ

x = sen ⁡ θ       ;       d x = cos ⁡ θ d θ

Assim, vamos ter o seguinte:

∫ x 2 1 - x 2 d x = ∫ sen ⁡ θ 2 1 - sen ⁡ θ 2 cos ⁡ θ d θ

= ∫ sen ⁡ θ 2 cos 2 ⁡ θ cos ⁡ θ d θ = ∫ sen ⁡ θ 2 cos ⁡ θ cos ⁡ θ d θ

Considerando cos ⁡ θ é positivo dentro da nossa substituição,

∫ sen ⁡ θ 2 cos ⁡ θ cos ⁡ θ d θ = ∫ sen 2 ⁡ θ d θ

Passo 2

Agora vamos abrir o seno ao quadrado por uma relação trigonométrica maneira:

∫ sen 2 ⁡ θ d θ = ∫ 1 - cos ⁡ 2 θ 2 d θ = θ 2 - sen ⁡ 2 θ 4

Onde sen ⁡ 2 θ = 2 sen ⁡ θ cos ⁡ θ , por outra relação trigonométrica:

= θ 2 - 2 sen ⁡ θ cos ⁡ θ 4

Agora desfazemos a substituição. Temos que sen ⁡ θ = x , o que gera θ = arcsen ⁡ x e:

cos ⁡ θ = 1 - sen ⁡ θ 2 = 1 - x 2

Logo,

θ 2 - 2 sen ⁡ θ cos ⁡ θ 4 = arcsen ⁡ x 2 - 2 x 1 - x 2 4 + C

Resposta

∫ x 2 1 - x 2 d x = arcsen ⁡ x 2 - 2 x 1 - x 2 4 + C

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x