Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 150123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

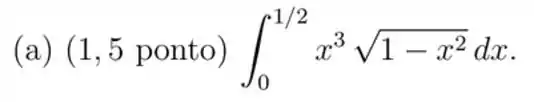
Passo 1

Aqui nós temos que usar a substituição trigonométrica esse é o caso da substituição do seno:

1 - x 2 = a 2 - x 2   →       x = a sen ⁡ θ

x = sen ⁡ θ       ;       d x = cos ⁡ θ d θ

Alteramos os limites de integração também:

x = 1 2 → sen ⁡ θ = 1 2 → θ = π 6

x = 0 → sen ⁡ θ = 0 → θ = 0

Assim, vamos ter o seguinte:

∫ 0 1 2 x 3 1 - x 2   d x = ∫ 0 π 6 sen ⁡ θ 3 1 - sen ⁡ θ 2   cos ⁡ θ d θ

= ∫ 0 π 6 sen ⁡ θ 3 cos ⁡ θ 2   cos ⁡ θ d θ = ∫ 0 π 6 sen ⁡ θ 3 cos ⁡ θ   cos ⁡ θ d θ

Entre 0 e π 6 , cos ⁡ θ é positivo e, com isso,

∫ 0 π 6 sen ⁡ θ 3 cos ⁡ θ   cos ⁡ θ d θ = ∫ 0 π 6 sen ⁡ θ 3 cos 2 ⁡ θ d θ

Passo 2

Agora vamos abrir o seno ao cubo em um seno ao quadrado multiplicado por seno:

∫ 0 π 6 sen ⁡ θ 3 cos 2 ⁡ θ d θ = ∫ 0 π 6 sen 2 ⁡ θ sen ⁡ θ cos 2 ⁡ θ d θ

Usamos a relação fundamental no seno ao quadrado:

∫ 0 π 6 1 - cos 2 ⁡ θ sen ⁡ θ cos 2 ⁡ θ d θ = ∫ 0 π 6 cos 2 ⁡ θ - cos 4 ⁡ θ sen ⁡ θ d θ

Substituindo o cosseno, saímos assim:

u = cos ⁡ θ       ;       d u = - sen ⁡ θ d θ

∫ 0 π 6 cos 2 ⁡ θ - cos 4 ⁡ θ sen ⁡ θ d θ = ∫ 0 π 6 u 2 - u 4 - d u

= u 5 5 - u 3 3 = cos 5 ⁡ θ 5 - cos 3 ⁡ θ 3 [ π 6 0 = cos 5 ⁡ π 6 5 - cos 3 ⁡ π 6 3 - cos 5 ⁡ 0 5 - cos 3 ⁡ 0 3

= 3 2 5 5 - 3 2 3 3 - 1 5 - 1 3 = ( c o n t i n h a s   c h a t a s … ) = 2 15 + 11 3 160

Resposta

∫ 0 1 2 x 3 1 - x 2   d x = 2 15 + 11 3 160

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x