Ache a área da região limitada pelos gráficos da parábola e a curva de Agnesi
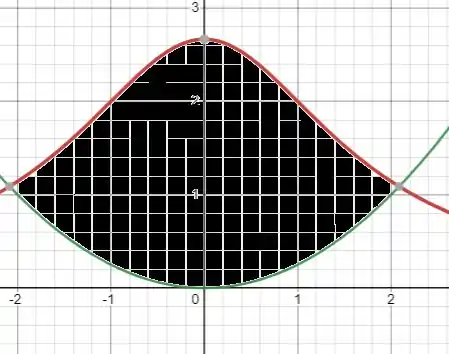
Passo 1
Faaaaaala, galera... Tranquileba?? Bora responder Aí essa questão?
Saca só: Quando queremos saber a região limitada por duas curvas, temos que saber os pontos onde ela s se interceptam. Nesse caso os é dado, mas e se não tivéssemos? Bom.. nesse caso vamos ver como é.
Basta igualar ambas as curvas, afinal queremos sabe os pontos onde elas são iguais. Logo:
Façamos
Aplicando bhaskara:
Logo não faz sentifo, não tem como o quadrado te um numero ser negativo, mas é possível, sim, assim:
E pronto, assim descobrimos os pontos onde essas curvas se interceptam e logo assim os limites de integração.
Para acharmos a área de uma região de interação, devemos fazer:
Sendo a e b os limites de integração
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Sendo f(x) a curva que rege a função, é a função superior menos a inferior, isto é nesse caso:
Assim a nossa área fica dada por fica:
Sabemos a soma das integrais é a integral da soma, assim:
Passo 3
Vamos separar essa integral em duas partes:
Para a primeira:
Fatorando o 4:
Nessa integral antes temos que fazer uma substituição que muda muita coisa. Geralmente essas integrais são resolvidas por uma substituição trigonométrica, geralmente são:
ou
Nesse caso vamos usar a segunda opção, sendo assim, façamos:
De forma que para dx:
E quando temos uma integral com os limtes definidos, se usamos uma substituição, qualquer que seja, os limites devem acompanhar a substituição que nós fizermos, isto quer dizer que quando:
E também quando:
Assim nossa integral fica:
Como demos antes, sabemos que Ficando ao final:
Realizando a integral:
Resumindo:
Para a segunda integral:
Passo 4
Assim, com as duas integrais já feitas, podemos obter:
E obtivemos nossa área.
Obrigado por ficar até aqui, carinha. Espero que tenha conseguido fazer também.