Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Substituição Trigonométrica

Ver Teoria
Exercício 137123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UnB; Cálculo 1; Lista 16; Exercício 1c

1) Calcule as integrais abaixo usando uma substituição trigonométrica adequada.

(c) ∫ ( x + 1 ) 4 - x 2   d x

Passo 1

Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!

O enunciado dessa questão já nos ajuda bastante! Ele afirma que temos que usar substituição trigonométrica. Então o que nos resta agora é determinar qual substituição trigonométrica vai se encaixar melhor na nossa situação aqui!

Meu deus, mas como fazemos isso mesmo?

Calma! Pra usarmos o método da substituição trigonométrica, é importante que a nossa função possua uma raiz com essa carinha aqui: x 2 + a 2 ,     x 2 - a 2 ,     a 2 - x 2 .

Olha só que legal, a nossa raiz presente ali na integral tem essa carinha!

∫ ( x + 1 ) 4 - x 2   d x

A gente pode ver ali que a 2 = 4 , então nosso a será igual a 2 !

Mas e agora o que eu faço com essa informação?

Vamos desenhar o nosso triângulo retângulo e fazer algumas interpretações!

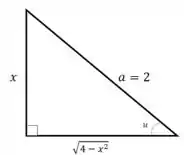
A partir disso, podemos fazer a seguinte relação trigonométrica:

x = 2 sin ⁡ u       ( I )

Disso, podemos obter sua derivada d x :

d x = 2 cos ⁡ ( u )   d u         ( I I )

A partir das equações I e   ( I I ) , podemos reescrever a nossa integral:

∫ 2 sin ⁡ ( u ) + 1   4 - 2 sin ⁡ u 2   2 cos ⁡ ( u )   d u

Bora lá trabalhar com isso então!

Passo 2

Vamos começar simplificando a nossa integral:

∫ 2 sin ⁡ ( u ) + 1 4 - 4  sin 2 ⁡ ( u )   2 cos ⁡ ( u )   d u

∫ 2 sin ⁡ ( u ) + 1 4 1 -  sin 2 ⁡ u   2 cos ⁡ ( u )   d u

∫ 2 sin ⁡ ( u ) + 1 2 1 -  sin 2 ⁡ u   2 cos ⁡ ( u )   d u

Vamos observar bem o nosso denominador agora. Você consegue ver a sacada que apareceu ali?

Temos uma identidade trigonométrica!!! Então, 1 - sin 2 ⁡ u = cos 2 ⁡ ( u )

Substituindo, vamos ter então:

∫ 2 sin ⁡ ( u ) + 1 2 cos 2 ⁡ ( u )   2 cos ⁡ ( u )   d u

∫ 2 sin ⁡ ( u ) + 1 2 cos ⁡ ( u )   2 cos ⁡ ( u )   d u

Podemos simplificar essa expressãozinha cancelando 2 cos ⁡ ( u ) :

∫ 2 sin ⁡ ( u ) + 1   d u

Olha só que simples!

Agora vamos dividir aquela integral já que temos uma soma, e tirar possíveis constantes de dentro da integral:

∫ 2 sin ⁡ ( u ) d u + ∫ 1   d u

2 ∫ sin ⁡ ( u ) d u + ∫ 1   d u

Vamos trabalhar com essas integrais no próximo passo agora!

Passo 3

Resolvendo então a primeira integral ali, vamos ter que:

2 ∫ sin ⁡ ( u ) d u = 2 - cos ⁡ u

Resolvendo a segunda integral, vamos ter que:

∫ 1   d u = u

Juntando isso, vamos ter como resultado:

2 - cos ⁡ u + u

Passo 4

Por fim, vamos determinar quem é nosso u . Pra isso, vamos voltar na nossa figura lá do passo 1, de onde podemos assumir que:

cos ⁡ ( u ) = 4 - x 2 2 ,     sin  ⁡ ( u ) = x 2

Além disso, vamos ter que:

u = arcsin ⁡ x 2

Então, substituindo isso no nosso resultado encontrado ali no passo 4, temos que:

arcsin ⁡ x 2 - 2 4 - x 2 2 + C

arcsin ⁡ x 2 - 4 - x 2 + C

Lembrando que esse C é a nossa constante de integração!

Ufa!! Conseguimos!!!!

Pra essa questão é isso pessoal! Bora pra mais uma?

Resposta

arcsin ⁡ x 2 - 4 - x 2 + C

Exercícios de Livros Relacionados

Encontre o volume do sólido obtido pela rotação em torno da reta x = 1 da região sob a curva y = 1 - x 2 , 0 ≤ x ≤ 1 .
Calcule a integral usando a substituição trigonométrica indicada. Esboce e coloque legendas no triângulo retângulo associado. ∫ x 3 9 - x 2 d x ; x = 3 sin ⁡ θ
Calcule a integral indefinida:int (x^2)/(sqrt(2 - x^2)) d x
Calcule a integral indefinida:int (5 x + 4)/(x^3 sqrt(x^2 + 1)) d x
Calcule a integralint (1)/(x^2 sqrt(4 x^2 - 1)) d x