1) Calcule as integrais abaixo usando uma substituição trigonométrica adequada.
(d)
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!

Como o enunciado dessa questão é bem direto e já afirma que teremos que resolver por substituição trigonométrica, o que nos resta agora é determinar qual substituição trigonométrica vai se encaixar na nossa funçãozinha! Meu deus, mas como fazemos isso mesmo?
Calma! Pra usarmos o método da substituição trigonométrica, é importante que a nossa função possua uma raiz com essa carinha aqui: .
Tá, mas a nossa função não tá lá muito parecida com isso não. O que eu faço?
Antes de qualquer desespero, o segredo pra esse exercício vai ser trabalhar com a nossa função! Então vamos começar dividindo a fração:
Como temos a soma de duas expressões, podemos ainda dividir essa integral:
Vamos então trabalhar em cada uma dessas integrais separadamente!
Bora lá então!
Passo 2
Pra resolvermos a primeira integral ali do passo 1, vamos começar tirando o 6 que é uma constante:
Agora, pra resolvermos essa integral, como temos um número em função de sendo dividido por outro número em função de x, não precisaremos utilizar substituição trigonométrica aqui!
Então, vamos adotar o método da substituição em :
Adotando e , vamos reescrever a nossa integral e já realizar a sua simplificação:
Olha só que expressão mais simples!! Agora está bem mais tranquilo de resolver essa primeira integralzinha!
Então, calculando-a, temos que:
Substituindo de volta, temos que:
Passo 3
Agora, vamos resolver a segunda integral ali do nosso passo 1:
Para resolvermos essa integral, como temos um número comum (sem estar em função de ), sendo dividido por outro que está em função de , precisaremos adotar o método da substituição trigonométrica!
Pra isso, vamos então desenhar o triângulo retângulo para fazer todas as relações para encontrarmos o resultado dessa integralzinha!
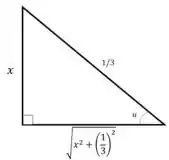
Antes de usarmos essa figura, vamos tirar o 5 de dentro da integral, já que ele é uma constante:
Pronto! Agora, a partir da figura, podemos estabelecer as seguintes relações:
Então a derivada de , é dada por:
Substituindo essas relações na nossa integral, e já simplificando, vamos ter que:
Olha só que interessante! Você consegue ver ali que temos uma sacada bem importante nessa expressão?
Podemos ver ali na raiz uma identidade trigonométrica!
Então:
Simplificando:
Como 1/3 é constante, podemos removê-lo da integral:
Lembrando que a integral acima já é conhecida e pode ser resolvida diretamente. Então, resolvendo essa integral vamos ter que:
Agora, podemos calcular o valor da secante pela figura lá do passo 1, já que o valor da tangente nós já temos.
Além dessa relação, encontrando essa expressão acima em função de , temos que:
Substituindo no nosso resultado ali em cima: , teremos:
Ufa! Achamos o valor da nossa segunda integral!
Passo 4
Por fim, vamos juntar as integrais obtidas nos passos 2 e 3 para obter nosso resultado final:
Lembrando que esse é a nossa constante de integração!
Conseguimos!!!! Amém!

Pra essa questão é isso pessoal! Bora pra mais uma?